
先化简,再求值: 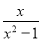 ÷(1+
÷(1+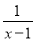 ),其中
),其中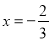 .
.
科目:初中数学 来源:江苏省南通市崇川区2016-2017学年七年级上学期期末考试数学试卷 题型:填空题
数轴上与表示-3的点相距4个单位长度的点表示的数是_____.
1或-7 【解析】【解析】 分为两种情况:①当点在表示﹣3的点的左边时,数为﹣3﹣4=﹣7; ②当点在表示﹣3的点的右边时,数为﹣3+4=1; 故答案为:1或﹣7.查看答案和解析>>
科目:初中数学 来源:黑龙江省安达市校2017-2018学年七年级上册期末教学质量检测数学试卷 题型:解答题
点A、B在数轴上分别表示有理数a、b,点A与原点O两点之间的 距离表示为AO,则AO=|a-0|=|a|,类似地,点B与原点O两点之间的距离表示 为BO,则BO=|b|,点A与点B两点之间的距离表示为AB=|a-b|.请结合数轴,思考并回答以下问题:
(1)①数轴上表示1和-3的两点之间的距离是__________;
②数轴上表示m和-1的两点之间的距离是__________;
③数轴上表示m和-1的两点之间的距离是3,则有理数m是___________;
(2)若x表示一个有理数,并且x比-3大,x比1小,则|x-1|+|x+3|=______;
(3)求满足|x-2|+|x+4|=6的所有整数x的和.

查看答案和解析>>
科目:初中数学 来源:黑龙江省安达市校2017-2018学年七年级上册期末教学质量检测数学试卷 题型:单选题
下列利用等式的性质,错误的是( )
A. 由a=b,得到5﹣2a=5﹣2b B. 由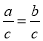 ,得到a=b
,得到a=b
C. 由a=b,得到ac=bc D. 由a=b,得到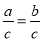
查看答案和解析>>
科目:初中数学 来源:黑龙江省安达市校2017-2018学年七年级上册期末教学质量检测数学试卷 题型:单选题
若a是有理数,则a+|a|( )
A. 可以是负数 B. 不可能是负数
C. 必是正数 D. 可以是正数也可以是负数
B 【解析】试题分析:分三种情况: 当a>0时,a+|a|=a+a=2a>0; 当a<0时,a+|a|=a-a=0; 当a=0时,a+|a|=0+0=0; ∴a+|a|是非负数, 故选B.查看答案和解析>>
科目:初中数学 来源:云南省2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
一艘轮船在静水中的速度为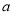 千米/时,水流速度为
千米/时,水流速度为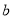 千米/时,若A、B两个港口之间的距离为50千米,则该轮船在A、B间往返一次所需时间为_________小时.
千米/时,若A、B两个港口之间的距离为50千米,则该轮船在A、B间往返一次所需时间为_________小时.
查看答案和解析>>
科目:初中数学 来源:云南省2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
用直尺和圆规作一个角等于已知角的示意图如图所示,则说明∠A′O′B′=∠AOB的依据是 ( )
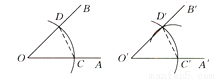
A. SSS B. SAS C. ASA D. AAS
A 【解析】根据用直尺和圆规作一个角等于已知角的示意图可知:OD=OD’,OC=OC’,CD=C’D’得 (SSS),得 . 故选A.查看答案和解析>>
科目:初中数学 来源:2017-2018学年度武汉市九年级元月联合测试数学试卷 题型:填空题
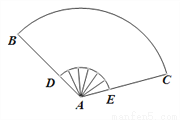
如图,扇形纸扇完全打开后,外侧面两竹条AB、AC夹角为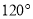 ,
, 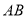 的长为
的长为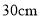 ,
, 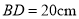 ,则扇面的面积为_____________cm2.
,则扇面的面积为_____________cm2.
查看答案和解析>>
科目:初中数学 来源:上海市青浦区2018届九年级上学期期末调研测试数学试卷 题型:解答题
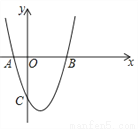
如图,在平面直角坐标系中,抛物线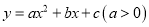 与
与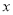 轴交于点
轴交于点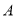 (?1,0)和点
(?1,0)和点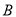 ,与
,与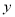 轴交于点
轴交于点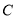 ,对称轴为直线
,对称轴为直线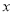 =1.
=1.
(1)求点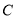 的坐标(用含
的坐标(用含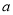 的代数式表示)
的代数式表示)
(2)连接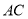 、
、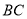 ,若△
,若△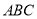 的面积为6,求此抛物线的解析式;
的面积为6,求此抛物线的解析式;
(3)在(2)的条件下,点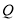 为
为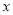 轴正半轴上的一点,点
轴正半轴上的一点,点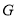 与点
与点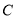 ,点
,点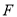 与点
与点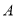 关于点
关于点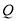 成中心对称,当△
成中心对称,当△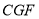 为直角三角形时,求点
为直角三角形时,求点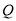 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com