
��������ε����߳��ֱ��Ƿ���x2��8x+15=0������������ô����������������ߵ��е㣬�õ��������ε��ܳ������ǣ� ��
A. 5.5 B. 5 C. 4.5 D. 4
A ������������������ⷽ��x2��8x+15=0�ã�x1=3��x2=5���������c�ķ�Χ�ǣ�2��c��8���������ε��ܳ�l�ķ�Χ�ǣ�10��l��16��������������������ߵ��е㣬�õ��������ε��ܳ�m�ķ�Χ�ǣ�5��m��8��������������ֻ��A����ѡA�� ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ�Ϸ���2016~17ѧ��ȵ�һѧ�� ��ĩ��ѧ������� ���꼶��ѧ�Ծ� ���ͣ������
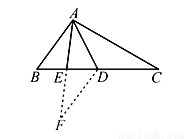
��֪����ͼ��AD��AE�ֱ��ǡ�ABC�͡�ABD�����ߣ���BA��BD����֤��AE��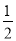 AC��
AC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ������꼶��ѧ�ϲ���ĩ���Ծ� ���ͣ���ѡ��
���������ǰ尴��ͼ��ʾ����ƴ��һ�����ABC���ڣ�������
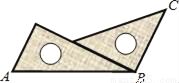
A. 70�� B. 90�� C. 105�� D. 120��
D ����������������� ��ѡD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����ɹ������첼�з�У���꼶���ϣ�������ѧ�Ծ� ���ͣ������
��A��1��4����B����2��1�����㣬�Գ���Ϊx=��1�������ߵĽ���ʽ_____��
y=x2+2x+1 ���������������߽���ʽΪy=ax2+bx+c�� ��������ã� , ��ã�a=1��b=2��c=1�� �������߽���ʽΪy=x2+2x+1�� �ʴ��ǣ�y=x2+2x+1.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����ɹ������첼�з�У���꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
��ͼ����ABO�У�AB��OB��OB=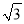 ��AB=1���ѡ�ABO�Ƶ�O��ת150���õ���A1B1O�����A1������Ϊ
��AB=1���ѡ�ABO�Ƶ�O��ת150���õ���A1B1O�����A1������Ϊ
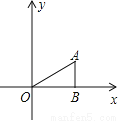
A. ����1�� 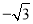 �� B. ����1��
�� B. ����1�� 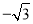 ����2��0�� C. ��
����2��0�� C. ��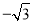 ����1����0����2�� D. ��
����1����0����2�� D. ��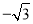 ����1��
����1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶���ϣ�������ѧ�Ծ� ���ͣ������
��֪����x�ķ���x2��2��k��1��x+k2=0������ʵ����x1��x2��
��1����k��ȡֵ��Χ��
��2����|x1+x2|=x1x2��1����k��ֵ��
��1��k�ܣ�3�֣��� ��2��k=-3��5�� �������������������1������������ʵ�������ɵá�=b2��4ac��0������ɽ��k��ȡֵ��Χ�� ��2����ϣ�1����k��ȡֵ��Χ���������֪��x1+x2=2��k��1����0��ȥ����ֵ�Ž�ϵ�ʽ��ϵ���ɵó�k��ֵ�� �������� ��1���ɷ���������ʵ�������ɵ� ��=b2��4ac=4��k��1��2��4k2=4k2��8k+4��4k2=��8k...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶���ϣ�������ѧ�Ծ� ���ͣ������
�������
��1��25x2+10x+1=0����ʽ���� ��2�� 7x2 -23x +6=0�����䷽����
(3) 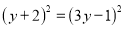 ���ֽ���ʽ���� ��4��x2-4x-396=0���ʵ��ķ�����
���ֽ���ʽ���� ��4��x2-4x-396=0���ʵ��ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
����x��һԪ���η��̣�m��2��x2+2x+1=0��ʵ��������m��ȡֵ��Χ�ǣ�������
A. m��3 B. m��3 C. m��3��m��2 D. m��3��m��2
D ���������������������x��һԪ���η��̣�m��2��x2��2x+1=0��ʵ������ô������ϵ��������0���������б�ʽ���ǷǸ������ɴ˿��Խ�������m�IJ���ʽ�飬�ⲻ��ʽ�鼴�����m��ȡֵ��Χ�� �������� �߹���x��һԪ���η��̣�m��2��x2��2x+1=0��ʵ���� ��m��2��0�����ҡ�=����2��2��4��m��2��=12��4m��0�� ��m��3��m��2�� ��ѡD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ������������2018����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ���ѡ��
˳������Խ�����ȵ��ı��ε��ı��е�����ͼ���ǣ�������
A. ������ B. ���� C. ���� D. ���϶�����
C �������������������ͼ��E��F��G��H�ֱ����ı���ABCD�ı�AB��BC��CD��DA���е㣬 ���������ε���λ�߶�����EF=AC��GH=AC��HE=BD��FG=BD�� ����AC��BD�� ���ı���ABCD�ĶԽ�����ȣ� ��AC=BD�� ���ԣ�EF=FG=GH=HE�� ���ԣ��ı���EFGH�����Σ� ��ѡC���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com