练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

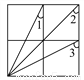
    如图，已知方格纸中是4个相同的正方形，则∠1＋∠2＋∠3＝____度．

    135 【解析】如图所示： 由题意可知△ABC≌△EDC， ∴∠3=∠BAC， 又∵∠1+∠BAC=90°， ∴∠1+∠3=90°， ∵DF=DC， ∴∠2=45°， ∴∠1+∠2+∠3=135度， 故答案是：135o．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：人教版九年级上册数学 24.4弧长和扇形面积（2）练习 题型：单选题

    制作一个底面直径为30 cm、高为40 cm的圆柱形无盖铁桶,所需铁皮至少为( )

    A. 1 425π cm2 B. 1 650π cm2 C. 2 100π cm2 D. 2 625π cm2

    A 【解析】试题解析：这个圆柱的底面直径是 所需铁皮就是一个底面积与侧面积的和. 故选A.

    查看答案和解析>>

    科目：初中数学 来源：《概率的进一步认识》单元测试4 题型：单选题

    下列说法正确的是（ ）

    A. 可能性很大的事件必然发生

    B. 可能性很小的事件也可能发生

    C. 如果一件事情可能不发生，那么它就是必然事件

    D. 如果一件事情发生的机会只有百分之一，那么它就不可能发生

    B 【解析】解：A．可能性很大的事件不是必然事件，不一定发生，故错误； B．可能性很小的事件也可能发生，很可能不发生，故正确； C．如果一件事情可能不发生，那么它就是随机事件，故错误； D．如果一件事情发生的机会只有百分之一，那么它也可能发生，很可能不发生，故错误． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质（2）测试 题型：单选题

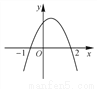
    抛物线的图象如图所示，根据图象可知，抛物线的解析式可能是( )

    A. y＝x2-x-2 B. y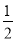＝-x2-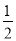x+2 C. y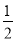＝-x2-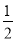x+1 D. y＝-x2+x+2

    D 【解析】A.由图象可知开口向下，故a<0，此选项错误； B.抛物线过点(?1，0)，(2，0)，根据抛物线的对称性，顶点的横坐标是，而的顶点横坐标是，故此选项错误； C. 的顶点横坐标是? ，故此选项错误； D. y=?x2+x+2的顶点横坐标是，并且抛物线过点(?1，0)，(2，0)，故此选项正确. 故选：D.

    查看答案和解析>>

    科目：初中数学 来源：天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习（含答案） 题型：填空题

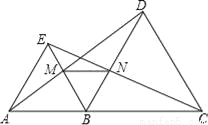
    如图，△ABE，△BCD均为等边三角形，点A，B，C在同一条直线上，连接AD，EC，AD与EB相交于点M，BD与EC相交于点N，下列说法正确的有：___________

    ①AD=EC；②BM=BN；③MN∥AC；④EM=MB．

    ①②③ 【解析】∵△ABE，△BCD均为等边三角形， ∴AB=BE，BC=BD，∠ABE=∠CBD=60°， ∴∠ABD=∠EBC， 在△ABD和△EBC中 ∴△ABD≌△EBC(SAS)， ∴AD=EC，故①正确； ∴∠DAB=∠BEC， 又由上可知∠ABE=∠CBD=60°， ∴∠EBD=60°， 在△ABM和△EBN中 ∴△A...

    查看答案和解析>>

    科目：初中数学 来源：天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习（含答案） 题型：填空题

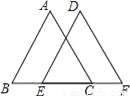
    △ABC和△FED中，BE=FC，∠A=∠D．当添加条件_________时（只需填写一个你认为正确的条件），就可得到△ABC≌△DFE，依据是________．

    ∠B=∠DEC AAS 【解析】添加∠B=∠DEC. ∵BE=FC， ∴BC=EF， 在△ABC和△DEF中， ， ∴△ABC≌△DEF(AAS)， 故答案为：∠B=∠DEC，AAS

    查看答案和解析>>

    科目：初中数学 来源：天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习（含答案） 题型：填空题

    如图，已知∠ACD=∠BCE，AC=DC，如果要得到△ACB≌△DCE，那么还需要添加的条件是______．（填写一个即可，不得添加辅助线和字母）

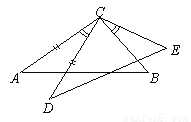
    ∠A=∠D或∠B=∠E或BC=EC 【解析】A=∠D， 理由是：∵∠ACD=∠BCE， ∴∠ACD+∠DCB=∠BCE+∠DCB， ∴∠ACB=∠DCE， 在△ACB和△DCE中， ∴△ACB≌△DCE(ASA)， 故答案为：∠A=∠D.

    查看答案和解析>>

    科目：初中数学 来源：天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习（含答案） 题型：填空题

    如图，Rt△ABC中，∠C=90°，AC=8，BC=4，PQ=AB，点P与点Q分别在AC和AC的垂线AD上移动，则当AP=_____________时，△ABC≌△APQ

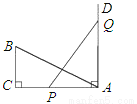
    8或4 【解析】要使，△ABC与△APQ全等， ∵PQ=AB,∠C=90?，AC⊥AD， ∴AP=BC=4， 或AP=AC=8， 所以，AP的长为4或8. 故答案为：4或8.

    查看答案和解析>>

    科目：初中数学 来源：北师大版（2012） 九年级上册同步练习：1.2矩形的性质 题型：填空题

    矩形ABCD中，M为AD的中点， MB ⊥MC， 矩形的周长为24， 则AB= _____， BC=_______．

    4, 8. 【解析】∵ABCD为矩形，∴AB=DC，∠D=∠A=90°， ∵点M是AD的中点，∴AM=DM，∴△ABM≌△DCM，∴BM=CM， ∵∠BMC=90°，∴△BMC为等腰直角三角形，∴AB=AM=AD， ∵矩形ABCD的周长是24， ∴2（AB+AD）=6AB=24， ∴AB=4，BC=AD=8， 故答案为：4，8．

    查看答案和解析>>

    同步练习册答案