
��ͼ����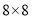 ������������ÿ��С�����εı߳�Ϊ
������������ÿ��С�����εı߳�Ϊ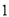 ������Ҫ����ͼ�����㣮
������Ҫ����ͼ�����㣮
��1����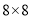 �������������н���ƽ��ֱ������ϵ��ʹ��
�������������н���ƽ��ֱ������ϵ��ʹ��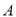 ������Ϊ
������Ϊ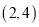 ����
����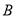 ������Ϊ
������Ϊ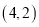 ��
��
��2������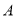 ����ƽ��
����ƽ��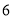 ����λ���ٹ���
����λ���ٹ���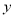 ��ԳƵõ���
��ԳƵõ���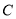 �����
�����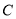 ���ꣻ
���ꣻ
��3������������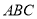 �����ж�
�����ж�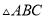 ����״��˵�����ɣ�
����״��˵�����ɣ�

 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡͭ�ʵ���ͭ����2017-2018ѧ�����꼶���ϣ�������ѧ�Ծ� ���ͣ������
����ʽ4yx2��2x��7��_____��_____��ʽ��
�� �� ������������ʽ4yx2��2x��7�Ĵ�����3����3������ʽ�ĺͣ������������ʽ����������ʽ�� �ʴ�Ϊ�����������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ������������2017-2018ѧ�����꼶��ѧ������ģ����ѧ�Ծ� ���ͣ���ѡ��
һ�����dz߰���ͼ��ʾ�ڷţ���֪ ��
�� ��3����10�㣬��
��3����10�㣬�� =�� ��
=�� ��

A. 20�� B. 70�� C. 25�� D. 65��
D ������������ͼʾ��֪��1+��2=90�㣬 ���������֪��1=3��2-10�㣬 ���ԡ�2=(90��+100��)��4=25�㣬���ԡ�1=65�㣬 ��ѡ��D. �㾦���⿼���˻����Լ�һԪһ�η��̵�Ӧ�ã��ҵ���1�͡�2֮��Ĺ�ϵ�ǽ������Ĺؼ�.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰������ѧ���꼶�ϲ�ڶ�ʮһ�µ�һ�ڡ�һԪ���η��̡�ͬ�����ԣ����𰸣� ���ͣ���ѡ��
��ax2��5x+3=0��һԪ���η��̣���ʽ3a+6��0�Ľ⼯Ϊ�� ��
A. a����2 B. a����2
C. a����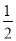 D. a����2��a��0
D. a����2��a��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭�����ຼ��2016-2017ѧ����꼶��ѧ����ĩ��ѧ�Ծ� ���ͣ������
��֪����ͼ�� 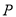 ��
��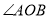 ��һ�㣬
��һ�㣬 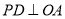 ��
�� 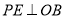 ��
�� 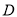 ��
�� 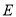 �ֱ��Ǵ��㣬��
�ֱ��Ǵ��㣬��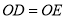 ��
��
�� ����֤����
����֤���� ��
��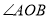 ��ƽ�����ϣ�
��ƽ�����ϣ�
��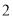 ������
������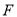 ������
������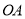 ��һ�㣬��
��һ�㣬��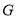 ������
������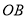 ��һ�㣬��
��һ�㣬��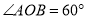 ��
�� 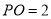 ��
��
�ٵ�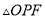 �ǵ���������ʱ�����
�ǵ���������ʱ�����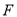 ������
������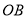 �ľ��룻
�ľ��룻
������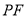 ��
�� 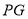 ��
�� 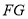 ����
����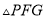 ���ܳ���Сʱ����
���ܳ���Сʱ����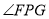 �Ķ�����
�Ķ�����
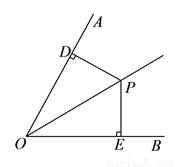
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭�����ຼ��2016-2017ѧ����꼶��ѧ����ĩ��ѧ�Ծ� ���ͣ������
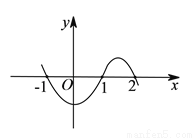
��֪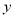 �ǹ���
�ǹ���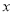 �ĺ���������ͼ����ͼ����
�ĺ���������ͼ����ͼ����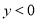 ʱ���Ա���
ʱ���Ա���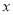 ��ȡֵ��Χ��__________��
��ȡֵ��Χ��__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭�����ຼ��2016-2017ѧ����꼶��ѧ����ĩ��ѧ�Ծ� ���ͣ���ѡ��
��ͼ��һֱ�����������������ֱ��� ��
��  ���㣬
���㣬 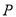 ���߶�
���߶�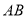 ������һ�㣨�������˵㣩������
������һ�㣨�������˵㣩������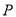 �ֱ�����������Ĵ�������������Χ�ɵij����ε��ܳ�Ϊ
�ֱ�����������Ĵ�������������Χ�ɵij����ε��ܳ�Ϊ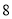 �����ֱ�ߵĺ�������ʽ�ǣ� ����
�����ֱ�ߵĺ�������ʽ�ǣ� ����
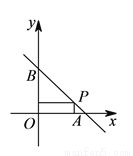
A. 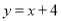 B.
B. 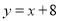
C. 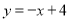 D.
D. 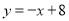
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ������2017-2018ѧ����꼶��ѧ��������ѧ�Ծ� ���ͣ������
���������ε�һ����ǵ���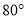 �������Ķ�����__________��
�������Ķ�����__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰�2017-2018ѧ�����꼶�²�5.2��ƽ���ߵ��ж��������ѧ�Ծ� ���ͣ���ѡ��
��ͼ�����������ĸ���������AC=BD���ڡ�DAC=��BCA���ۡ�ABD=��CDB���ܡ�ADB=��CBD��������ʹAD��BC�������ǣ� ��
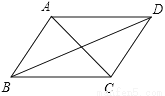
A. �٢� B. �ۢ� C. �ڢ� D. �٢ۢ�
C ����������AC=BD�������ж���ֱ��ƽ�У��ʴ��ڡ�DAC=��BCA�������ڴ�����ȣ���ֱ��ƽ�пɵ�AD��BC������ȷ���ۡ�ABD�͡�CDB��ֱ��AB��CD��BD�����γɵ��ڴ��ǣ��ʿɵ�AB��CD���ʴ��ܡ�ADB=��CBD�������ڴ�����ȣ���ֱ��ƽ�пɵ�AD��BC������ȷ���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com