
方程x2﹣3x﹣4=0的解是__.
x1=﹣1,x2=4. 【解析】x2﹣3x﹣4=0, (x-4)(x+1)=0, x-4=0,x+1=0, 所以x1=-1,x2=4.科目:初中数学 来源:郑州二中学区2017-2018学年上学期期中学业水平测试 八年级数学试卷 题型:填空题
在平面直角坐标系中,已知一次函数y=2x+1的图象经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则y1 ______ y2.(填“>”“<”或“=”)
【答案】<
【解析】试题解析:∵一次函数y=2x+1中k=2>0,
∴y随x的增大而增大,
∵x1<x2,
∴y1<y2.
考点:一次函数图象上点的坐标特征.
【题型】填空题
【结束】
13
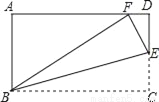
如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为_____.
查看答案和解析>>
科目:初中数学 来源:天津市 2017-2018学年 九年级数学上册 一元二次方程 因式分解法 专题练习(含答案) 题型:解答题
解方程:x2-2x-3=0.(因式分解法)
x1=3,x2=-1. 【解析】x2-2x-3=0. (x-3)(x+1)=0, x-3=0,x+1=0, x1=3,x2=-1.查看答案和解析>>
科目:初中数学 来源:天津市 2017-2018学年 九年级数学上册 一元二次方程 因式分解法 专题练习(含答案) 题型:解答题
解方程:(2x﹣1)2﹣9=0.(因式分解法)
x1=2,x2=﹣1. 【解析】(2x﹣1)2﹣9=0, (2x﹣1-3)( 2x﹣1+3)=0, (2x﹣4)( 2x+2)=0 所以x1=2,x2=﹣1.查看答案和解析>>
科目:初中数学 来源:天津市 2017-2018学年 九年级数学上册 一元二次方程 因式分解法 专题练习(含答案) 题型:填空题
方程x2﹣6x+9=0的解是______.
x1=x2=3. 【解析】试题分析:此题采用因式分解法最简单,解题时首先要观察,然后再选择解题方法.配方法与公式法适用于所用的一元二次方程,因式分解法虽有限制,却最简单.因此可得: ∵x2﹣6x+9=0 ∴(x﹣3)2=0 ∴x1=x2=3.查看答案和解析>>
科目:初中数学 来源:天津市 2017-2018学年 九年级数学上册 一元二次方程 因式分解法 专题练习(含答案) 题型:填空题
方程3(x-5)2=2(x-5)的根是__
x1=5,x2= 【解析】试题解析:方程变形得:3(x-5)2-2(x-5)=0, 分解因式得:(x-5)[3(x-5)-2]=0, 可得x-5=0或3x-17=0, 解得:x1=5,x2=.查看答案和解析>>
科目:初中数学 来源:江苏省句容市片区合作共同体2017-2018学年年八年级上学期第二次学情测试数学试卷 题型:解答题
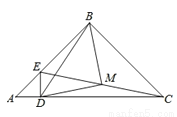
已知在△ABC中,AB=BC=8cm,∠ABC=90°,点E以每秒1cm/s的速度由A向点B运动,ED⊥AC于点D,点M为EC的中点.
(1)求证:△BMD为等腰直角三角形;
(2)当点E运动多少秒时,△BMD的面积为12.5cm2?
查看答案和解析>>
科目:初中数学 来源:江苏省句容市片区合作共同体2017-2018学年年八年级上学期第二次学情测试数学试卷 题型:填空题
地球的半径约为6.4×103km,这个近似数精确到__________位.
百. 【解析】∵近似数6.4×103=6400, ∴4在百位上,则近似数6.4×103精确到百位, 故答案为:百.查看答案和解析>>
科目:初中数学 来源:2017-2018学年上学期苏州市初三数学期末综合检测 题型:解答题
如图,四边形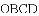
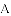
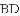
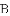
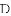
(1)当圆心
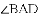
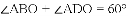
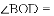
(2)当圆心
(3)当圆心
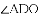
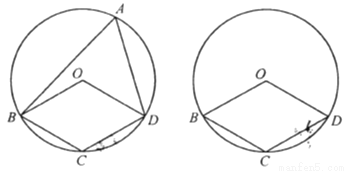
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com