
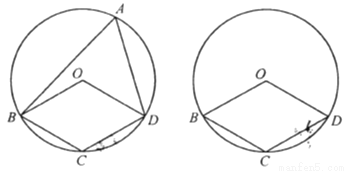
如图,四边形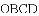
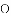
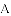
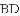
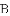
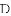
(1)当圆心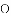
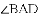
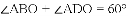
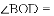
(2)当圆心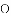
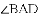
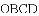
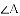
(3)当圆心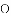
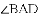
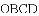
科目:初中数学 来源:天津市 2017-2018学年 九年级数学上册 一元二次方程 因式分解法 专题练习(含答案) 题型:填空题
方程x2﹣3x﹣4=0的解是__.
x1=﹣1,x2=4. 【解析】x2﹣3x﹣4=0, (x-4)(x+1)=0, x-4=0,x+1=0, 所以x1=-1,x2=4.查看答案和解析>>
科目:初中数学 来源:2017年甘肃省中考数学模拟试卷 题型:解答题
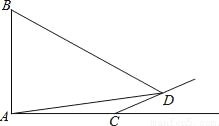
如图,旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处,某校数学课外兴趣小组的同学正在测量旗杆的高度,在旗杆的底部A处测得点D的仰角为15°,AC=10米,又测得∠BDA=45°.已知斜坡CD的坡度为i=1: 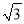 ,求旗杆AB的高度(
,求旗杆AB的高度( ,结果精确到个位).
,结果精确到个位).
查看答案和解析>>
科目:初中数学 来源:2017年甘肃省中考数学模拟试卷 题型:单选题
在一个不透明的布袋中,红色、黑色、白色的玻璃球共有60个,除颜色外,形状、大小、质地等完全相同.小刚通过多次摸球实验后发现其中摸到红色、黑色球的频率稳定在0.15和0.45,则口袋中白色球的个数很可能是( )个.
A. 12 B. 24 C. 36 D. 48
B 【解析】试题解析:∵小刚通过多次摸球实验后发现其中摸到红色、黑色球的频率稳定在0.15和0.45, ∴估计摸到红色、黑色球的概率分别为0.15和0.45, ∴摸到白球的概率为1-0.15-0.45=0.4, ∴口袋中白色球的个数为60×0.4=24, 即口袋中白色球的个数很可能24个. 故选B.查看答案和解析>>
科目:初中数学 来源:2017年甘肃省中考数学模拟试卷 题型:单选题
如图,1,2,3,4,T是五个完全相同的正方体,将两部分构成一个新的几何体得到其正视图,则应将几何体T放在( )
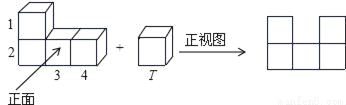
A. 几何体1的上方 B. 几何体2的左方
C. 几何体3的上方 D. 几何体4的上方
D 【解析】试题解析:由新几何体的主视图易得第二层最右边应有1个正方体,那么T应在几何体4的上方, 故选D.查看答案和解析>>
科目:初中数学 来源:2017-2018学年上学期苏州市初三数学期末综合检测 题型:解答题
解方程:
(1) 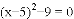 ;
;
(2) 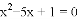 (用配方法);
(用配方法);
(3) 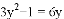
(4) 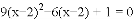
查看答案和解析>>
科目:初中数学 来源:2017-2018学年上学期苏州市初三数学期末综合检测 题型:填空题
已知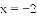
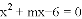 的一个根,则
的一个根,则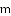
查看答案和解析>>
科目:初中数学 来源:山东省聊城市莘县2017-2018学年八年级(上)期中数学试卷 题型:填空题
如图,已知△ABC的面积是20,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的周长是_____.
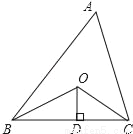
查看答案和解析>>
科目:初中数学 来源:内蒙古鄂尔多斯市2017-2018学年第一学期期中试卷初一数学. 题型:解答题
某国际化学校实行小班制教学,七年级四个班共有学生(6m-3n)人,一班有学生m人,二班人数比一班人数的两倍少n人,三班人数比二班人数的一半多12人.
(1)求三班的学生人数(用含m.n的式子表示);
(2)求四班的学生人数;(用含m.n的式子表示) ;
(3)若四个班共有学生120人,求二班比三班多的学生人数?
(1)一班m人,二班()人,三班()人;(2)四班()人;(3)二班比三班多8人. 【解析】试题分析: (1)由一班有学生m人,根据二班人数比一班人数的两倍少n人得出二班(2m-n)人,根据(2m-n)人得出三班为(+12)人; (2)利用四个班共有学生(6m-3n)人减去三个班人数得出四班的人数; (3)把120代入6m-3n,求得m、n的关系,进一步列出二班比三班多的人数,整...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com