练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若﹣3xm+7y2与2x5yn的和仍为单项式，则mn=__________；

    4 【解析】试题解析：根据题意可得： 是同类项. 则： 故答案为：4.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：黑龙江省哈尔滨市双城区2017-2018学年八年级上学期期末考试数学试卷 题型：单选题

    已知等腰三角形两边长是8cm和4cm，那么它的周长是（　　）

    A. 12cm B. 16cm C. 16cm或20cm D. 20cm

    D 【解析】【解析】 当腰为4cm时，4+4=8，不能构成三角形，因此这种情况不成立． 当腰为8cm时，8＜8+4，能构成三角形； 此时等腰三角形的周长为8+8+4=20cm． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：吉林省第二实验学校2017-2018学年七年级（上）期中数学试卷 题型：解答题

    计算题：

    （1）（﹣14）﹣（+15）；

    （2）﹣3﹣4+19﹣11+2；

    （3）（﹣4）﹣（﹣1）+（﹣6）+2；

    （4）6÷（-2）+（+3）×；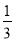

    （5） ．

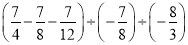    （1）﹣29；（2）3；（3）﹣7；（4）﹣2；（5）． 【解析】试题分析：（1）原式利用减法法则变形，计算即可求出值； （2）原式结合后相加即可求出值； （3）原式利用减法法则变形计算即可求出值； （4）原式先计算乘除运算，再计算加减运算即可求出值； （5）原式利用除法法则变形，计算即可求出值． 试题解析：【解析】 （1）原式=﹣14﹣15=﹣29； ...

    查看答案和解析>>

    科目：初中数学 来源：甘肃省武威市2017-2018学年七年级上学期期末考试数学试卷 题型：解答题

    如图，OD是∠AOB的平分线，OE是∠BOC的平分线，且∠AOC=130°，求∠DOE的度数．

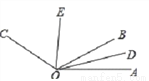
    ∠DOE =65°． 【解析】试题分析：利用角平分线的定义得出进而求出的度数． 试题解析：∵OD是∠AOB的平分线,OE是∠BOC的平分线,且 ∴∠AOD=∠BOD，∠BOE=∠COE，

    查看答案和解析>>

    科目：初中数学 来源：甘肃省武威市2017-2018学年七年级上学期期末考试数学试卷 题型：填空题

    将矩形ABCD沿AE折叠，得到如图的图形．已知∠CEB′=50°，则∠AEB′=__°．

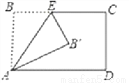
    65 【解析】根据折叠前后对应部分相等得∠AEB′=∠AEB，再由已知求解． 【解析】 ∵∠AEB′是△AEB沿AE折叠而得， ∴∠AEB′=∠AEB． 又∵∠BEC=180°，即∠AEB′+∠AEB+∠CEB′=180°， 又∵∠CEB′=50°， ∴∠AEB′==65°， 故答案为：65．

    查看答案和解析>>

    科目：初中数学 来源：甘肃省武威市2017-2018学年七年级上学期期末考试数学试卷 题型：单选题

    已知︱x︱＝2，y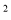=9,且x·y<0,则x＋y=( )

    A. ±1 B. -1 C. -5或-1 D. 5

    A 【解析】试题解析： 且 则 故选A．

    查看答案和解析>>

    科目：初中数学 来源：江苏省2018届九年级下学期模拟考试数学试卷 题型：解答题

    二次函数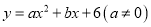的图像交y轴于C点，交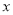轴于A，B两点（点A在点B的左侧），点A、点B的横坐标是一元二次方程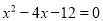的两个根．

    （1）求出点A、点B的坐标及该二次函数表达式．

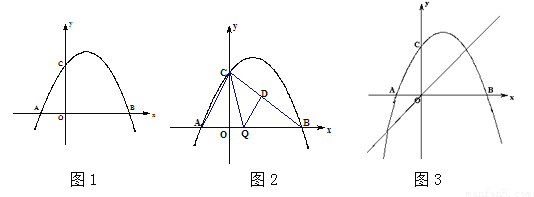
    （2）如图2，连接AC、BC，点Q是线段OB上一个动点（点Q不与点O、B重合），过点Q作QD∥AC交于BC点D，设Q点坐标（m，0），当△CDQ面积S最大时，求m的值．

    （3）如图3，线段MN是直线y=x上的动线段（点M在点N左侧），且MN=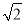，若M点的横坐标为n，过点M作x轴的垂线与x轴交于点P，过点N作x轴的垂线与抛物线交于点Q．以点P，M，Q，N为顶点的四边形能否为平行四边形？若能，请求出n的值；若不能，请说明理由．

    （1）A（－2，0），B（6，0），；（2）；（3）n=1±或-1±． 【解析】试题分析：（1）解一元二次方程x2-4x-12=0可求A、B两点坐标；将A、B两点坐标代入二次函数y=ax2+bx+6，可求二次函数解析式； （2）由DQ∥AC得△BDQ∽△BCA，利用相似比表示△BDQ的面积，利用三角形面积公式表示△ACQ的面积，根据S△CDQ=S△ABC-S△BDQ-S△ACQ，运用二...

    查看答案和解析>>

    科目：初中数学 来源：江苏省2018届九年级下学期模拟考试数学试卷 题型：填空题

    已知，则的值是_______．

    5 【解析】因为，所以=8-（a-3b）=8-3=5

    查看答案和解析>>

    科目：初中数学 来源：内蒙古赤峰市宁城县2017-2018学年七年级上学期期末考试数学试卷 题型：解答题

    探究归纳题：

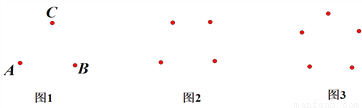
    (1)试验分析：

    如图1，经过A点与B、C两点分别作直线，可以作____________条；同样，经过B点与A、C两点分别作直线，可以作______________条；经过C点与A、B两点分别作直线，可以作___________条.

    通过以上分析和总结，图1共有___________条直线.

    （2）拓展延伸：

    运用（1）的分析方法，可得：

    图2共有_____________条直线；

    图3共有_____________条直线；

    (3)探索归纳：

    如果平面上有n(n≥3)个点，且每3个点均不在同一直线上，经过其中两点共有________条直线．(用含n的式子表示)

    (4)解决问题：

    中职篮（CBA）2017——2018赛季作出重大改革，比赛队伍数扩充为20支，截止2017年12月21日赛程过半，即每两队之间都赛了一场，请你帮助计算一下一共进行了多少场比赛？

    （1）2 2 2 3 （2）6 10 （3）（4）190 【解析】试题分析：（1）、（2）根据两点确定一条直线即可得出结论； （3）由（2）可得出结论； （4）根据（3）列式求值即可. 试题解析：（1）2；2；2；3； （2）6；10； （3） （4）当n=20时， =（场）. 故一共进行了190场比赛.

    查看答案和解析>>

    同步练习册答案