
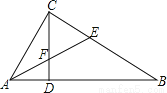
如图,已知Rt△ABC中,∠ACB=90°,CD⊥AB于D,∠BAC的平分线分别交BC、CD于E、F.试说明△CEF是等腰三角形.
 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源:山西省吕梁市孝义市2016-2017学年九年级(上)期末考试数学试卷 题型:解答题
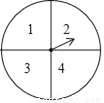
元旦期间,某商场设置了如图所示的幸运转盘,转盘分成4个大小相同的扇形,分别标有数学1,2,3,4,指针的位置固定,转盘可以自由转动,当转动的转盘停止后,其中的某个扇形会停在指针所指的位置(指针指向两个扇形的交线时,当作右边的扇形).商场规定:凡是参加抽奖的顾客均可转动转盘两次,如果两次转动中指针指缶扇形上的数字之和为8是一等奖,数字之和为7是二等奖,数字之和为6是三等奖,标号之和为其他数字则获得一份纪念品,请分别求出顾客抽中一、二、三等奖的概率.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年黑龙江省大庆市杜尔伯特县九年级(上)期末数学试卷(五四学制) 题型:单选题
若关于x的函数y=(2﹣a)x2﹣x是二次函数,则a的取值范围是( )
A. a≠0 B. a≠2 C. a<2 D. a>2
B 【解析】试题解析:∵函数y=(2-a)x2-x是二次函数, ∴2-a≠0,即a≠2, 故选B.查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学北师大版上册:第4章 基本平面图形 单元测试卷 题型:单选题
如图,点C在线段AB上,点D是AC的中点,如果CD=3cm,AB=10cm,那么BC的长度是( )

A. 3cm B. 3.5cm C. 4cm D. 4.5cm
C 【解析】试题分析:根据线段中点的定义求出AC,再根据BC=AB﹣AC计算即可得解. 【解析】 ∵点D是AC的中点, ∴AC=2CD=2×3=6cm, ∴BC=AB﹣AC=10﹣6=4cm. 故选C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学北师大版上册:第4章 基本平面图形 单元测试卷 题型:单选题
如图,C是线段AB的中点,D是CB上一点,下列说法中错误的是( )
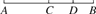
A. CD=AC-BD B. CD=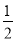 BC C. CD=
BC C. CD=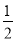 AB-BD D. CD=AD-BC
AB-BD D. CD=AD-BC
查看答案和解析>>
科目:初中数学 来源:山东省德州地区2017-2018学年度第一学期期末检测八年级数学试卷 题型:填空题
如图,点P是∠AOB内部的一点,∠AOB=30°,OP=8 cm,M,N是OA,OB上的两个动点,则△MPN周长的最小值_____cm.
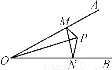
查看答案和解析>>
科目:初中数学 来源:山东省德州地区2017-2018学年度第一学期期末检测八年级数学试卷 题型:单选题
某厂接到加工720件衣服的订单,预计每天做48件,正好按时完成,后因客户要求提前5天交货,设每天应多做x件才能按时交货,则x应满足的方程为( )
A. 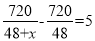 B.
B. 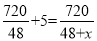
C. 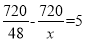 D.
D. 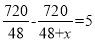
查看答案和解析>>
科目:初中数学 来源:广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型:解答题
已知抛物线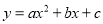 经过点A(1,0),B(-1,0),C(0,-2).求此抛物线的函数解析式和顶点坐标.
经过点A(1,0),B(-1,0),C(0,-2).求此抛物线的函数解析式和顶点坐标.
查看答案和解析>>
科目:初中数学 来源:广西合浦县2017年秋季学期教学质量监测七年级数学试卷 题型:解答题
一个不透明的口袋里装有分别标有汉字“美”、“丽”、“南”、“山”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,求摸出球上的汉字刚好是“美”的概率;
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图或列表法,求甲取出的两个球上的汉字恰能组成“美丽”或“南山”的概率.
(1) P=;(2) P= 【解析】分析:(1)由一个不透明的口袋里装有分别标有汉字“美”、“丽”、“南”、“山”的四个小球,除汉字不同之外,小球没有任何区别,直接利用概率公式求解即可求得答案; (2)首先根据题意列举出所有可能的结果与取出的两个球上的汉字恰能组成“美丽”或“南山”的情况,再利用概率公式即可求得答案. 本题解析: (1)∵有汉字“美”、“丽”、“南”、“山”...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com