
在△ABC中,若cosB=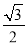 ,tanA=
,tanA=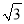 ,且∠A、∠B为锐角,则△ABC是_________三角形.
,且∠A、∠B为锐角,则△ABC是_________三角形.
科目:初中数学 来源:江苏省丹阳市2017-2018学年七年级12月月考数学试卷 题型:填空题
方程(2a-1)x2+3x+1=4是一元一次方程,则a= ______ .
【解析】由题意得2a-1=0,解得a= .查看答案和解析>>
科目:初中数学 来源:吉林省松原市2018届九年级上期末模拟数学试卷 题型:填空题
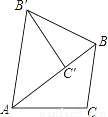
如图,把△ABC绕点A逆时针旋转42°,得到△AB′C′,点C′恰好落在边AB上,连接BB′,则∠B′BC′的大小为________.
查看答案和解析>>
科目:初中数学 来源:湖南省邵阳县黄亭市2017~2018学年九年级数学(上)期末检测模拟题 题型:解答题
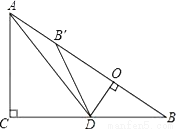
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.
(1)求证:△DOB∽△ACB;
(2)若AD平分∠CAB,求线段BD的长;
(3)当△AB′D为等腰三角形时,求线段BD的长.
查看答案和解析>>
科目:初中数学 来源:湖南省邵阳县黄亭市2017~2018学年九年级数学(上)期末检测模拟题 题型:解答题
解方程:(1)3x2-6x+6=0;(2)2(x-3) 2=x2-9.
(1)无解;(2)x1=3,x2=9. 【解析】试题分析:(1)利用公式法.(2)利用因式分解法解方程. 试题解析: (1)3x2-6x+6=0; x2-2x+2=0, a=1,b=-2,c=2, 无解. (2)2(x-3) 2=x2-9, 2(x-3) 2=(x-3)(x+3), 2(x-3) 2-(x-3)(x+3)=0 (x-3)(...查看答案和解析>>
科目:初中数学 来源:湖南省邵阳县黄亭市2017~2018学年九年级数学(上)期末检测模拟题 题型:单选题
如图,在△ABC 中,∠BAC=90°,AB=AC,点 D 为边AC 的中点,DE⊥BC 于点E,连接BD,则tan∠DBC 的值为 ( )
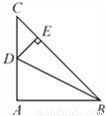
A. 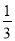 B.
B. 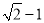 C.
C. 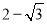 D.
D. 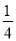
查看答案和解析>>
科目:初中数学 来源:湖南省邵阳县黄亭市2017~2018学年九年级数学(上)期末检测模拟题 题型:单选题
方程2x2=3(x-6)化为一般形式二次项系数、一次项系数和常数项分别为 ( )
A. 2,3,-6 B. 2,-3,18 C. 2,-3,6 D. 2,3,6
B 【解析】试题分析:要确定一次项系数和常数项,首先要把方程化成一般形式. 【解析】 方程2x2=3(x﹣6), 去括号,得2x2=3x﹣18, 整理,得2x2﹣3x+18=0, 所以,二次项系数、一次项系数、常数项分别是2,﹣3,18, 故选B.查看答案和解析>>
科目:初中数学 来源:湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型:单选题
25的算术平方根是( )
A. 5 B. -5 C. ±5 D. 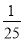
查看答案和解析>>
科目:初中数学 来源:2017年安徽省六安市金安区滨河学校中考数学模拟试卷 题型:填空题
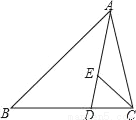
在△ABC中,∠B=45°,点D在边BC上,AD=AC,点E在边AD上,∠BCE=45°,若AB=5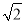 ,AE=2DE,则AC=_____.
,AE=2DE,则AC=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com