练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，平面内有公共端点的六条射线OA、OB、OC、OD、OE、OF，从射线OA开始按逆时针依次在射线上写出数字1、2、3、4、5、6、7…，则数字“2008”在（　　）

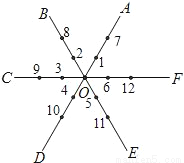
    A. 射线OA上 B. 射线OB上 C. 射线OD上 D. 射线OF上

    C 【解析】观察图形可得,按照逆时针方向,每6个数字为一个循环组,2008÷6=334……4,所以,数字2008是第335组的第4个数字,在射线OD上,故选C.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：人教版数学七年级下册（贵州专版） 期中综合检测 题型：填空题

    如图，请你填写一个适当的条件： ，使AD∥BC．

    ∠FAD=∠FBC（答案不唯一） 【解析】 试题分析：根据同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行中的任意的一个判定定理都可以进行说明.

    查看答案和解析>>

    科目：初中数学 来源：初一数学第一学期4.3角同步练习 题型：填空题

    用度、分、秒表示91.34°为________.

    【解析】试题分析：因为0．34°=0．34×60′=20．4′，而0．4′=0．4×60″=24″，所以91．34°=91°20′24″．

    查看答案和解析>>

    科目：初中数学 来源：初一数学第一学期4.1线段、直线、射线 同步练习 题型：解答题

    已知四点A、B、C、D，按照下列语句画出图形；

    （1）作线段AD，并以cm为单位，度量其长度；

    （2）线段AC和线段DB相交于点O；

    （3）反向延长线段BC至E，使BE=BC．

    图形见解析 【解析】试题分析:(1)根据线段的定义,连接AD,即可得线段AD,然后用直尺量出AD的长度即可,(2)根据线段的定义和题目要求,连接AC和BD,两线段的交点即为点O,(3)根据反向延长线的定义,沿CB方向延长,使得BE的长度等于BC即可. 试题解析:如图所示,AD=3.5cm,

    查看答案和解析>>

    科目：初中数学 来源：初一数学第一学期4.1线段、直线、射线 同步练习 题型：填空题

    如图，图中有__条直线，有__条射线，有__条线段，以E为顶点的角有__个．

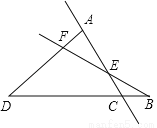
    1 9 12 4 【解析】如图,图中有直线AC,共1条直线,有A为端点的2条射线,B为端点的1条射线,C为端点的2条射线,E为端点的3条射线,F为端点的1条射线,共9条射线,有线段AC,AD,AE,AF,BC,BD,BE,BF,CD,CE,DF,EF,共12条线段,以E为顶点的角有∠AEB,∠AEF, ∠BEC,∠CEF,共4个,故答案为:1,9,12,4.

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 23.2.2中心对称图形 测试 题型：解答题

    如图，已知四边形ABCD和点P，用尺规作出四边形ABCD关于点P的对称四边形A′B′C′D′（保留作图痕迹）

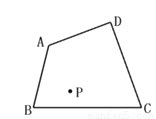
    作图见解析 【解析】试题分析：连接AP并延长到A′，使PA′=PA，则A′即为A的对应点，按此方法可依次找到B，C，D的对应点B′，C′，D′，顺次连接即可得到四边形ABCD关于原点P 对称的图形． 试题解析：如图所示：四边形A′B′C′D′和四边形ABCD关于点P对称．

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 23.2.2中心对称图形 测试 题型：单选题

    下列标志图中，既是轴对称图形，又是中心对称图形的是（　）

    A. B. C. D.

    B 【解析】试题解析：A、∵此图形旋转180°后能与原图形重合，∴此图形是中心对称图形，不是轴对称图形，故A选项错误； B、∵此图形旋转180°后能与原图形重合，∴此图形是中心对称图形，也是轴对称图形，故B选项正确； C、此图形旋转180°后不能与原图形重合，此图形不是中心对称图形，是轴对称图形，故C选项错误； D、∵此图形旋转180°后不能与原图形重合，∴此图形不是中心对...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年第一学期人教版八年级数学上11.2.1《三角形的内角和》同步练习题（含答案） 题型：单选题

    在△ABC中,∠B=40°,∠C=80°,则∠A的度数为( )

    A. 30° B. 40° C. 50° D. 60°

    D 【解析】由三角形内角和定理得∠A=180°?∠B?∠C=180°?40°?80°=60°， 故选：D.

    查看答案和解析>>

    科目：初中数学 来源：山西省大同市矿区2017-2018学年八年级上学期期中考试数学试卷 题型：单选题

    如图，在△ABC中，AB=AC，D为 BC 的中点，连接AD，那么以下结论不正确的是（　　）

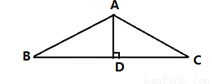
    A. △ABD≌△ACD B. ∠B=∠C

    C. AD是△ABC的高 D. AD不是△ABC的角平分线

    D 【解析】∵在△ABC中，AB=AC，D为BC中点， ∴∠B=∠C，AD⊥BC，AD平分∠BAC， ∴AD是△ABC的高，△ABD≌△ACD（HL）， 由此可知选项A、B、C都是正确的，只有D是错误的. 故选D.

    查看答案和解析>>

    同步练习册答案