
如图,等腰三角形ABC的顶点A在原点,顶点B在x轴的正半轴上,顶点C在函数y=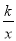 (x>0)的图象上运动,且AC=BC,则△ABC的面积大小变化情况是( )
(x>0)的图象上运动,且AC=BC,则△ABC的面积大小变化情况是( )
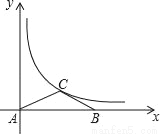
A. 一直不变 B. 先增大后减小 C. 先减小后增大 D. 先增大后不变
A 【解析】 作CD⊥AB交AB于点D, 则S△ACD=, ∵AC=BC, ∴AD=BD, ∴S△ACD=S△BCD, ∴S△ABC=2 S△ACD=2×=k. ∴△ABC的面积不变. 故选A.科目:初中数学 来源:黑龙江省哈尔滨市香坊区2017年中考数学二模试卷(解析版) 题型:单选题
已知点A(2,y1)、B(4,y2)都在反比例函数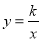 (k<0)的图象上,则y1、y2的大小关系为( )
(k<0)的图象上,则y1、y2的大小关系为( )
A. y1>y2 B. y1<y2 C. y1=y2 D. 无法确定
B 【解析】试题分析:∵当k<0时,y=在每个象限内,y随x的增大而增大,∴y1<y2,故选B.查看答案和解析>>
科目:初中数学 来源:广州市2018学年度七年级(上)数学期末测试卷 题型:单选题
若有理数a,b满足|3-a|+(b+2)2=0,则a+b的值为
A. 1 B. ﹣1 C. 5 D. ﹣5
A 【解析】试题解析:由题意得,3-a=0,b+2=0, 解得a=3,b=?2, 所以,a+b=3+(?2)=1. 故选A.查看答案和解析>>
科目:初中数学 来源:2017年甘肃省兰州市中考数学模拟试卷 题型:解答题
计算:|1﹣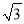 |+3tan30°﹣(
|+3tan30°﹣(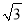 ﹣5)0﹣(﹣
﹣5)0﹣(﹣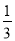 )﹣1.
)﹣1.
查看答案和解析>>
科目:初中数学 来源:2017年甘肃省兰州市中考数学模拟试卷 题型:单选题
如图,点A为∠α边上任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )
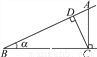
A. 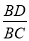 B.
B. 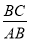 C.
C. 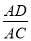 D.
D. 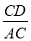
查看答案和解析>>
科目:初中数学 来源:2017年甘肃省兰州市中考数学模拟试卷 题型:单选题
如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形OCED的周长为( )
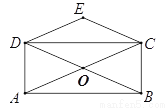
A. 4 B. 8 C. 10 D. 12
B 【解析】由四边形ABCD为矩形,得到OD=OC,再利用平行四边形的判定得到四边形DECO为平行四边形,利用菱形的判定定理得到四边形DECO为菱形,根据AC的长求出OC的长,即可确定出其周长. 【解析】 ∵四边形ABCD为矩形, ∴OA=OC,OB=OD,且AC=BD, ∴OA=OB=OC=OD=2, ∵CE∥BD,DE∥AC, ∴四边形DECO为平行四边形...查看答案和解析>>
科目:初中数学 来源:甘肃省武威市2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
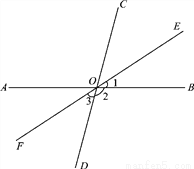
如图,直线AB、CD相交于点O,∠BOC=80°,OE是∠BOC的角平分线,OF是OE的反向延长线.
(1)求∠2、∠3的度数;
(2)说明OF平分∠AOD的理由.
查看答案和解析>>
科目:初中数学 来源:甘肃省武威市2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
几个人共同种一批树苗,如果每人种5棵,则剩下3棵树苗未种;如果每人种6棵,则缺4棵树苗.若设参与种树的人数为x人,则下面所列方程中正确的是( )
A. 5x+3=6x﹣4 B. 5x+3=6x+4 C. 5x﹣3=6x﹣4 D. 5x﹣3=6x+4
A 【解析】利用所种树苗的总数相等列方程. 每人种5棵,则剩下3棵树苗未种,则树苗总数为:5x+3; 每人种6棵,则缺4棵树苗,则树苗总数为:6x-4. 所以有:5x+3=6x-4. 故选A.查看答案和解析>>
科目:初中数学 来源:湖北省襄阳市襄城区2016-2017学年度上学期期末考试八年级数学试卷 题型:解答题
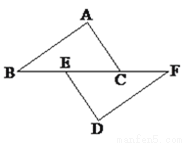
如图,已知,点B,E,C,F在一条直线上,AB=DF,AC=DE,∠A=∠D.
(1)求证:AC∥DE;
(2)若BF=21,EC=9,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com