某市创建“绿色发展模范城市”，针对境内长江段两种主要污染源：生活污水和沿江工厂污染物排放，分别用“生活污水集中处理”（下称甲方案）和“沿江工厂转型升级”（下称乙方案）进行治理，若江水污染指数记为Q，沿江工厂用乙方案进行一次性治理（当年完工），从当年开始，所治理的每家工厂一年降低的Q值都以平均值n计算．第一年有40家工厂用乙方案治理，共使Q值降低了12．经过三年治理，境内长江水质明显改善．
（1）求n的值；
（2）从第二年起，每年用乙方案新治理的工厂数量比上一年都增加相同的百分数m，三年来用乙方案治理的工厂数量共190家，求m的值，并计算第二年用乙方案新治理的工厂数量；
（3）该市生活污水用甲方案治理，从第二年起，每年因此降低的Q值比上一年都增加个相同的数值a．在（2）的情况下，第二年，用乙方案所治理的工厂合计降低的Q值与当年因甲方案治理降低的Q值相等，第三年，用甲方案使Q值降低了39.5．求第一年用甲方案治理降低的Q值及a的值．
阅读快车系列答案科目：初中数学 来源：2018秋人教版（广西专版）八年级数学上册第十二章质量评估测试卷 题型：单选题
如图，点A，D，C，E在同一条直线上，AB∥EF，AB＝EF，∠B＝∠F，AE＝10，AC＝7，则CD的长为( )
A. 5.5 B. 4 C. 4.5 D. 3
查看答案和解析>>
科目：初中数学 来源：2018年秋九年级上册 数学 第二章 一元二次方程 单元测试卷 题型：填空题
某药品原价每盒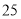
元，为了响应国家解决老百姓看病贵的号召，经过连续两次降价，现在售价每盒
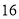元，则该药品平均每次降价的百分率是______．
查看答案和解析>>
科目：初中数学 来源：2018年秋九年级上册 数学 第二章 一元二次方程 单元测试卷 题型：单选题
某学习小组共同探究代数式x2﹣4x+5的值的情况，得到如下结论，其中错误的是（ ）
A. 当x取大于2的实数时，x2﹣4x+5的值随x的增大而增大，因此认为没有最大值
B. x2﹣4x+5的值随x的变化而变化，因此认为没有最小值
C. 找不到实数x，使x2﹣4x+5 的值为0
D. 只有当x=2时，x2﹣4x+5的值为1
查看答案和解析>>
科目：初中数学 来源：2018届人教版九年级上册数学 第21章 一元二次方程 单元测试卷 题型：解答题
已知：关于x的一元二次方程x2﹣（2m+3）x+m2+3m+2=0．
（1）已知x=2是方程的一个根，求m的值；
（2）以这个方程的两个实数根作为△ABC中AB、AC（AB＜AC）的边长，当BC=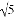
时，△ABC是等腰三角形，求此时m的值.
查看答案和解析>>
科目：初中数学 来源：2018届人教版九年级上册数学 第21章 一元二次方程 单元测试卷 题型：单选题
一元二次方程x2﹣2x=0的两根分别为x1和x2，则x1x2为（ ）
A. ﹣2 B. 1 C. 2 D. 0
查看答案和解析>>
科目：初中数学 来源：2019届湘教版九年级数学下册单元测试(一) 二次函数(B卷) 题型：单选题
如图，二次函数y＝ax2＋bx＋c(a＞0)图象的顶点为D，其图象与x轴的交点A，B的横坐标分别为－1和3，则下列结论正确的是( )
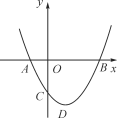
A. 2a－b＝0 B. a＋b＋c＞0
C. 3a－c＝0 D. 当a＝
时，△ABD是等腰直角三角形
查看答案和解析>>
科目：初中数学 来源：2018年秋人教版九年级上册数学 第25章 概率初步 单元测试卷 题型：填空题
新定义运算“◎”，对于任意有理数a、b，都有a◎b=a2﹣ab+b﹣1，例如：3◎5=32﹣3×5+5﹣1=﹣2，若任意投掷一枚印有数字1～6的质地均匀的骰子，将朝上的点数作为x的值，则代数式（x﹣3）◎（3+x）的值为非负数的概率是_____．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，则m的值为_____．