
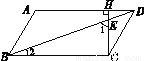
如图,在□ABCD中,CH⊥AD于点H, CH与BD的交点为E.如果∠1=70°,∠ABC=3∠2,那么∠ADC= ________
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源:江苏省东部分校2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
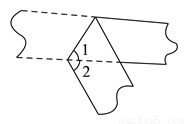
如图,将一张纸张折叠,若∠1=65°,则∠2的度数为____.
查看答案和解析>>
科目:初中数学 来源:江苏省泰兴市2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
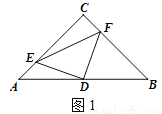
如图,△ABC中,AC=BC,∠C=90°,点D是AB的中点.
(1)如图1,若点E、F分别是AC、BC上的点,且AE=CF,请判别△DEF的形状,并说明理由;
(2)若点E、F分别是CA、BC延长线上的点,且AE=CF,则(1)中的结论是否仍然成立?请
说明理由.
查看答案和解析>>
科目:初中数学 来源:江苏省泰兴市2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
一次函数y=kx+b(k≠0)的图象如图所示,则一元一次不等式-kx+b>0的的解集为( )
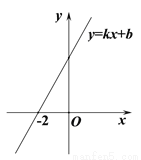
A. 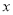 >-2 B.
>-2 B. 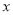 <-2 C.
<-2 C. 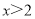 D.
D. 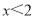
查看答案和解析>>
科目:初中数学 来源:北师大版八年级数学上册 第七章 平行线的证明 单元测试 题型:解答题
已知:如图,E、F是平行四边行ABCD的对角线AC上的 两点,AE=CF。
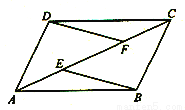
求证:(1)△ADF≌△CBE
(2)EB∥DF.
∵四边形ABCD为平行四边形, ∴AD∥BC,AD=BC. ………………(1分) ∴∠DAC=∠BCE. 又∵AE=CF,∴AF=CE ∴△ADF≌△CBE.……………………(4分) ∴∠AFD=∠CEB. ∴BE∥DF. ……………………………(6分 【解析】试题分析:要证△ADF≌△CBE,因为AE=CF,则两边同时加上EF,得到AF=CE,又因为AB...查看答案和解析>>
科目:初中数学 来源:北师大版八年级数学上册 第七章 平行线的证明 单元测试 题型:填空题
已知命题“如果一个四边形是平行四边形,那么这个四边形是旋转对称图形.”,写出它的逆命题是 ,该逆命题是 命题(填“真”或“假”).
如果一个四边形是旋转对称图形,那么这个四边形是平行四边形,真. 【解析】试题分析: “如果一个四边形是平行四边形,那么这个四边形是旋转对称图形”的逆命题是“如果一个四边形是旋转对称图形,那么这个四边形是平行四边形”.该逆命题是真命题.查看答案和解析>>
科目:初中数学 来源:北师大版八年级数学上册 第七章 平行线的证明 单元测试 题型:单选题
下列条件中,能判定△ABC为直角三角形的是( )
A. ∠A=2∠B=3∠C B. ∠A+∠B=2∠C
C. ∠A=∠B=30° D. ∠A= ∠B=
∠B=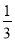 ∠C
∠C
查看答案和解析>>
科目:初中数学 来源:四川省宜宾市2017-2018学年上学期期末教学质量监测八年级数学试卷 题型:填空题
若 那么
那么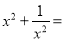 __________.
__________.
查看答案和解析>>
科目:初中数学 来源:北师大版数学九年级上册第一章特殊平行四边形第二节《矩形的性质与判定》课时练习 题型:解答题
如图,在△ABC中,AB=AC=5,BC=6,AD为BC边上的高,过点A作AE∥BC,过点D作DE∥AC,AE与DE交于点E,AB与DE交于点F,连结BE.求四边形AEBD的面积
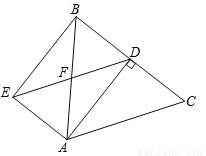
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com