
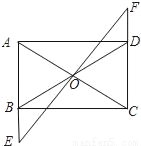
��ͼ������ABCD�У�O��AC��BD�Ľ��㣬��O���ֱ��EF��AB��CD���ӳ��߷ֱ���E��F��
��1����֤����BOE�ա�DOF��
��2����EF��AC����ʲô��ϵʱ����A��E��C��FΪ������ı��������Σ�֤����Ľ��ۣ�

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017�꽭��ʡ̩�����п���ѧ��ģ�Ծ� ���ͣ������
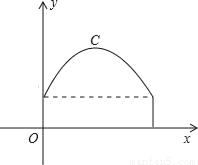
��ͼ�������Ľ����������ߺͳ����ι��ɣ������εij���8m������2m�������ߵ���ߵ㵽·��ľ���Ϊ6�ף�
��1������ͼ��ʾ����ƽ��ֱ������ϵ�����ʾ�������ߵĺ�������ʽ��
��2��һ�����˿�����Ϊ4m����Ϊ2m���������������˫������ô���������ܷ�ȫͨ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ������������У����2018����꼶��ѧ����ĩѧҵ�����ѧ�Ծ� ���ͣ���ѡ��
��֪���κ�����ͼ��0��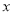 ��4����ͼ�����ڸú����������Ա�����ȡֵ��Χ�ڣ�����˵����ȷ���ǣ� ��
��4����ͼ�����ڸú����������Ա�����ȡֵ��Χ�ڣ�����˵����ȷ���ǣ� ��
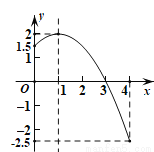
A. �����ֵ2������Сֵ-2.5 B. �����ֵ2������Сֵ1.5
C. �����ֵ1.5������Сֵ-2.5 C�������ֵ2������Сֵ
A ����������ͼ���֪����x=1ʱ��y�����ֵ2;��x=4ʱ��y����Сֵ-2.5. ��ѡA.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�긣��ʡ������ܼ��������ѧУ���꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
һ�л�m�ף���ÿ��n���ٶ�ͨ��һ����Ϊp���Ŷ����ô���ʽ��ʾ��ͨ���Ŷ������ʱ��Ϊ�� ��
A. 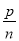 �� B.
�� B. 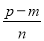 �� C.
�� C. 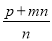 �� D.
�� D. 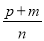 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�긣��ʡ������ܼ��������ѧУ���꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
��2�ľ���ֵ�ǣ�������
A. ��2 B. 2 C. ��2 D. 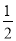
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�����ɹ�ͨ���а��꼶���£���ĩ��ѧ�Ծ� ���ͣ������
�ҹ�������ѧ����ˬΪ��֤�����ɶ�����������һ������ͼ�������˳���Ϊ����ˬ��ͼ������ͼ1����ͼ2����ͼ�仯�õ��������ɰ˸�ȫ�ȵ�ֱ��������ƴ�Ӷ��ɣ���ͼ��������ABCD��������EFGH��������MNKT������ֱ�ΪS1��S2��S3����S1+S2+S3=10����S2��ֵ��_________��
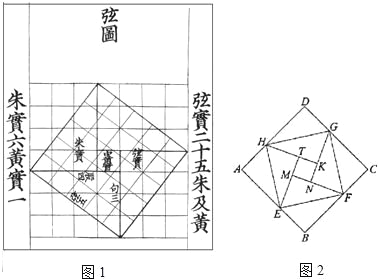
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�����ɹ�ͨ���а��꼶���£���ĩ��ѧ�Ծ� ���ͣ���ѡ��
үүÿ��������������ij����������ҵ���ɽ��������һ���̫��ȭ�������ؼң������ܷ�ӳ����С����үү��ҵľ���y��ʱ��x�ĺ�����ϵ�Ĵ���ͼ���ǣ�������
A. 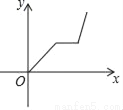 B.
B. 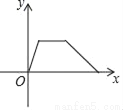 C.
C. 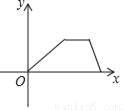 D.
D. 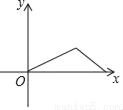
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����ɹų�������꼶���ϣ�������ѧ�Ծ� ���ͣ������
��|a+2|+��b��3��2=0����5a2b��[3ab2��2��ab��2.5a2b��+ab]+4ab2��ֵ��
ab2+ab,-24 ������������������Ƚ�ԭʽȥ���š��ϲ�ͬ��������ʽ���ٸ��ݷǸ��������ʵó�a��b��ֵ�����������ɵã� ����������������� ԭʽ=5a2b��3ab2+2��ab��2.5a2b����ab+4ab2 =5a2b��3ab2+2ab��5a2b��ab+4ab2 =ab2+ab ��|a+2|+��b��3��2=0����a+2=0��b��3=0����a=��2��b=3...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��ƽ��2018����꼶��ѧ�ڵڶ����¿���ѧ�Ծ� ���ͣ������
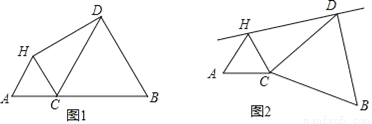
��ͼ��CΪ�߶�AB��һ�㣬�ֱ���AC��BCΪ����AB��ͬ�����ȱߡ�HAC��ȱߡ�DCB������DH.
��1����ͼ1������DHC=90��ʱ����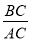 ��ֵ��
��ֵ��
��2���ڣ�1���������£�����C����ֱ��DH�ĶԳƵ�E������AE��BE.��֤��CEƽ�֡�AEB.
��3���ֽ�ͼ1�еġ�DCB�Ƶ�C˳ʱ����תһ���ǶȦ���0��<��<90�㣩����ͼ2����C����ֱ��DH�ĶԳƵ�ΪE����2���еĽ����Ƿ�������֤��.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com