
碳纳米管的硬度与金刚石相当,却拥有良好的柔韧性,可以拉伸,我国某物理所研究组已研制出直径为0.5纳米的碳纳米管,1纳米=0.000000001米,则0.5纳米用科学记数法表示为( )
A. 0.5×10–9米 B. 5×10–8米 C. 5×10–9米 D. 5×10–10米
D 【解析】【解析】 0.5纳米=0.5×0.000 000 001米=0.000 000 000 5米=5×10﹣10米. 故选D. 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型:解答题
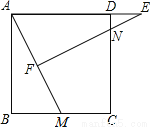
如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM ∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
科目:初中数学 来源:江苏省泰州市2017年中考数学二模试卷(解析版) 题型:填空题
函数y=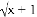 中,自变量x的取值范围是_____.
中,自变量x的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源:2017年河南省中考数学三模试卷 题型:填空题
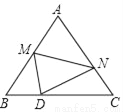
如图,等边△ABC的边长为10,点M是边AB上一动点,将等边△ABC沿过点M的直线折叠,该直线与直线AC交于点N,使点A落在直线BC上的点D处,且BD:DC=1:4,折痕为MN,则AN的长为_____.
查看答案和解析>>
科目:初中数学 来源:2017年河南省中考数学三模试卷 题型:填空题
已知函数y=(k﹣3)x2+2x+1的图象与x轴有交点,则k的取值范围是( )
A. k<4 B. k≤4 C. k<4且k≠3 D. k≤4且k≠3
B 【解析】试题分析:(1)当k-3=0,即k=3时,函数y=2x+1的图象与x轴有交点;(2)当时,二次函数y=(k-3)x2+2x+1的图象与x轴有交点,则,所以k≤4,所以k≤4且k≠3,由(1)(2)可知,当k≤4时,函数y=(k-3)x2+2x+1的图象与x轴有交点,故选:B.查看答案和解析>>
科目:初中数学 来源:湖北省黄冈市2017-2018学年七年级上学期第三次学力检测数学试卷 题型:单选题
随着服装市场竞争日益激烈,某品牌服装专卖店一款服装按原售价降价a元后,再次降价20%,现售价为b元,则原售价为( )
A. (a+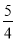 b)元 B. (a+
b)元 B. (a+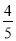 b)元 C. (b+
b)元 C. (b+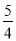 a)元 D. (b+
a)元 D. (b+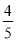 a)元
a)元
查看答案和解析>>
科目:初中数学 来源:湖北省黄冈市2017-2018学年七年级上学期第三次学力检测数学试卷 题型:单选题
下列各对数是互为倒数的是( )
A. 4和-4 B. -3和 C. -2和
C. -2和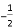 D. 0和0
D. 0和0
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区保俶塔实验学校2018届九年级上学期期中考试数学试卷(含解析) 题型:单选题
有一座圆弧形的拱桥,桥下水平宽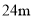 ,拱顶高出水平面
,拱顶高出水平面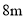 ,现有一货船,送一箱货欲从桥下经过,已知货箱(货箱底与水平面持平)宽
,现有一货船,送一箱货欲从桥下经过,已知货箱(货箱底与水平面持平)宽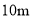 ,至多能截( )
,至多能截( )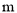 的货.
的货.
A. 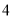 B.
B. 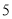 C.
C. 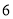 D.
D. 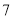
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2017-2018学年八年级上册期末模拟数学试卷 题型:填空题
m的6倍与4的差不小于12,列不等式为________.
6m﹣4≥12 【解析】首先表示“m的6倍与4的差”为6m﹣4,再表示“不小于12”可得6m﹣4≥12. 故答案为:6m﹣4≥12.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com