
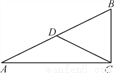
如图,在Rt△ABC中,∠ACB=90°,AB=10 cm,D为AB的中点,则CD=____________ cm.
科目:初中数学 来源:黄金30题系列 九年级数学 小题好拿分 题型:单选题
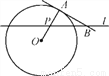
如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与过A点的⊙O的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )
A. 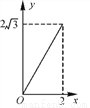 B.
B. 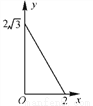 C.
C. 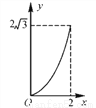 D.
D. 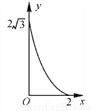
查看答案和解析>>
科目:初中数学 来源:2017年广东省东莞市堂星晨学校考数学模拟试卷 题型:填空题
如图,已知点A、B、C、D均在以BC为直径的圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10,则图中阴影部分的面积为__.
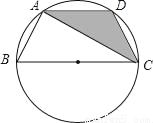
查看答案和解析>>
科目:初中数学 来源:2018年春人教版八年级数学下册(广西)期中测试 题型:解答题
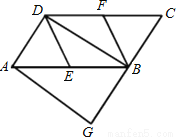
如图,在平行四边形ABCD中,∠DAB=60°,AB=2AD,点 E、F分别是AB、CD的中点,过点A作AG∥BD,交CB的延长线于点G.
(1)求证:四边形DEBF是菱形;
(2)请判断四边形AGBD是什么特殊四边形?并加以证明.
查看答案和解析>>
科目:初中数学 来源:2018年春人教版八年级数学下册(广西)期中测试 题型:填空题
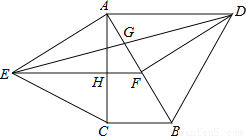
如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH=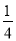 BD
BD
其中正确结论的为______(请将所有正确的序号都填上).
查看答案和解析>>
科目:初中数学 来源:2018年春人教版八年级数学下册(广西)期中测试 题型:单选题
已知菱形的周长为4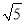 ,两条对角线的和为6,则菱形的面积为( )
,两条对角线的和为6,则菱形的面积为( )
A. 2 B. 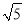 C. 3 D. 4
C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源:2018年春人教版八年级数学下册(广西)期中测试 题型:单选题
若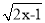 在实数范围内有意义,则x的取值范围是( )
在实数范围内有意义,则x的取值范围是( )
A. x≥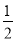 B. x≥-
B. x≥-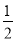 C. x>
C. x>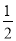 D. x≠
D. x≠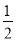
查看答案和解析>>
科目:初中数学 来源:青海省2017-2018学年七年级上学期12月月考数学试卷 题型:解答题
先化简,再求值:x2+(2xy-3y2)-2(x2+yx-2y2),其中x=-1,y=2.
原式=﹣x2+y2,当x=﹣1,y=2时,原式=3. 【解析】试题分析:先根据去括号、合并同类项化简,然后再把x、y的值代入求解; 【解析】 x2+(2xy﹣3y2)﹣2(x2+yx﹣2y2), =x2+2xy﹣3y2﹣2x2﹣2yx+4y2, =﹣x2+y2, 当x=﹣1,y=2时, 原式=﹣(﹣1)2+22=﹣1+4=3.查看答案和解析>>
科目:初中数学 来源:甘肃省定西市安定区2017-2018学年九年级上学期期末考试数学试卷 题型:单选题
将抛物线y=x2-4x-4向左平移3个单位,再向上平移5个单位,得到抛物线的表达式为( )
A. y=(x+1)2-13 B. y=(x-5)2-3 C. y=(x-5)2-13 D. y=(x+1)2-3
A 【解析】先将一般式化为顶点式,根据左加右减,上加下减来平移 【解析】 将抛物线化为顶点式为: ,左平移3个单位,再向上平移5个单位 得到抛物线的表达式为 故选A. “点睛”本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com