练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    （2a3b2-10a4c ）÷ 2a3等于（ ）

    A. a6b2c B. a5b2c C. b2-5ac D. b4c -a4c

    C 【解析】（2a3b2-10a4c ）÷ 2a3=2a3b2÷ 2a3-10a4c÷ 2a3= b2-5ac, 故选：C.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年九年级数学北师大版上册 全册综合测试卷2 题型：解答题

    数学活动——探究特殊的平行四边形．

    问题情境

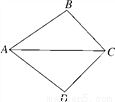
    如图，在四边形ABCD中，AC为对角线，AB=AD，BC=DC.请你添加条件，使它们成为特殊的平行四边形．

    提出问题

    (1)第一小组添加的条件是“AB∥CD”，则四边形ABCD是菱形．请你证明；

    (2)第二小组添加的条件是“∠B=90°，∠BCD=90°”，则四边形ABCD是正方形．请你证明．

    （1）证明见解析；（2）证明见解析. 【解析】试题分析：（1）根据SSS可判定△ABC≌△ADC，根据全等三角形对应角相等和两直线平行内错角相等可得∠BAC=∠DCA=∠BCA=∠DAC，根据等角对等边可得AB=BC=CD=DA，即得结论；（2）由△ABC≌△ADC得∠D =∠B=90°，又∠BCD=90°，可判定四边形BCD是矩形，又因BC=DC，即可得出结论． 试题解析：（1）∵A...

    查看答案和解析>>

    科目：初中数学 来源：江苏省苏州市张家港市2016-2017学年九年级（上）期末数学试卷 题型：单选题

    若点M（﹣1，y1），N（1，y2），P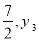（）都在抛物线y=﹣mx2+4mx+m2+1（m＞0）上，则下列结论正确的是（　　）

    A. y1＜y2＜y3 B. y1＜y3＜y2 C. y3＜y1＜y2 D. 2＜y1＜y3

    B 【解析】观察二次函数的图象可知：y1＜y3＜y2． 故选：B.

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级下册第一章整式乘法1.7整式的除法课时练习 题型：填空题

    （2a3b2+8a2c）÷2a2等于_______；

    ab2+4c 【解析】（2a3b2+8a2c）÷2a2=2a3b2÷2a2+8a2c÷2a2= ab2+4c, 故答案为：ab2+4c.

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级下册第一章整式乘法1.7整式的除法课时练习 题型：单选题

    （4x2y4+4x2z ） ÷（2x）2等于（ ）

    A. 4y4+z B. －y4+z C. y4+x2z D. y4+z

    D 【解析】（4x2y4+4x2z ） ÷（2x）2=（4x2y4+4x2z ） ÷4x2=4x2y4÷4x2+4x2z ÷4x2= y4+x2z， 故选：D.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下3.1 用表格表示的变量间关系 同步练习 题型：解答题

    心理学家发现,学生对概念的接受能力y与提出概念所用的时间x(单位:min)之间有如下关系(其中0≤x≤20):

    提出概念所

    用时间x/min

    2

    5

    7

    10

    12

    13

    14

    17

    20

    对概念的接

    受能力y

    47.8

    53.5

    56.3

    59

    59.8

    59.9

    59.8

    58.3

    55

    　(注:接受能力值越大,说明学生的接受能力越强)

    (1)上表中反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?

    (2)当提出概念所用时间是10 min时,学生的接受能力是多少?

    (3)根据表格中的数据,你认为提出概念所用时间为多少时,学生的接受能力最强?

    (4)从表格中可知,当提出概念所用时间x在什么范围内时,学生的接受能力逐步增强?当提出概念所用时间x在什么范围内时,学生的接受能力逐步降低?

    (1)反映了提出概念所用的时间x和对概念的接受能力y两个变量之间的关系;其中x是自变量,y是因变量. (2) 59. (3)所用时间为13 min时,学生的接受能力最强. (4)当x在2至13的范围内,学生的接受能力逐步增强;当x在13至20的范围内,学生的接受能力逐步降低. 【解析】分析：(1)由条件可知两个变量是提出概念所用的时间和对概念的接受能力，对概念的接受能力随着...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下3.1 用表格表示的变量间关系 同步练习 题型：单选题

    一个圆柱的高h为10 cm,当圆柱的底面半径r由小到大变化时,圆柱的体积V也发生了变化,在这个变化过程中(　　)

    A. r是因变量,V是自变量 B. r是自变量,V是因变量

    C. r是自变量,h是因变量 D. h是自变量,V是因变量

    B 【解析】圆柱的高h＝10厘米，因此h是常量不是变量，故排除C、D，圆柱的体积V随底面圆半径r的变化而变化，所以r是自变量，V是因变量. 故答案为：B.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学人教版5.1相交线同步练习 题型：单选题

    如图，直线AB，CD相交于点O，OA平分∠COE，∠COE＝70°，则∠BOD的度数是（ ）

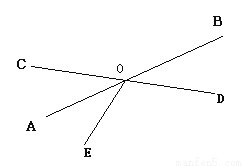
    A. 20° B. 30° C. 35° D. 40°

    C 【解析】首先利用相交线的性质确定对顶角相等，然后根据角平分线定义得出所求角与已知角的关系转化求解． 【解析】 ∵∠COE=70°且OA平分∠COE， ∴∠COA=∠COE=35°， 又∵∠COA与∠BOD是对顶角， ∴∠BOD = ∠COA =35°. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下册 第二章 相交线与平行线 2.2 探索直线平行的条件 同位角及平行公理 同步课堂练习题 题型：单选题

    如图，直线AB、CD被直线EF所截，则∠AMN的同位角是( )

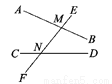
    A. ∠CNM B. ∠CNF C. ∠DNF D. ∠DNM

    B 【解析】∵直线AB、CD被直线EF所截， ∴只有∠AMN与∠CNF在截线EF的同侧，且在AB和CD的同旁， 即∠CNF是∠AMN的同位角。 故选B.

    查看答案和解析>>

    同步练习册答案