
如图,四边形ABCD是边长为2,一个锐角等于60°的菱形纸片,小芳同学将一个三角形纸片的一个顶点与该菱形顶点D重合,按顺时针方向旋转三角形纸片,使它的两边分别交CB、BA(或它们的延长线)于点E、F,∠EDF=60°,当CE=AF时,如图1小芳同学得出的结论是DE=DF.
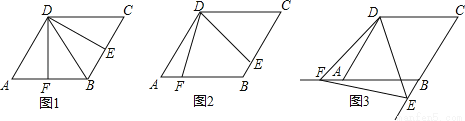
(1)继续旋转三角形纸片,当CE≠AF时,如图2小芳的结论是否成立?若成立,加以证明;若不成立,请说明理由;
(2)再次旋转三角形纸片,当点E、F分别在CB、BA的延长线上时,如图3请直接写出DE与DF的数量关系;
(3)连EF,若△DEF的面积为y,CE=x,求y与x的关系式,并指出当x为何值时,y有最小值,最小值是多少?
(1)成立,证明见解析;(2)DF=DE.(3)当x=0时,y最小值=. 【解析】 试题分析:(1)如图1,连接BD.根据题干条件首先证明∠ADF=∠BDE,然后证明△ADF≌△BDE(ASA),得DF=DE; (2)如图2,连接BD.根据题干条件首先证明∠ADF=∠BDE,然后证明△ADF≌△BDE(ASA),得DF=DE; (3)根据(2)中的△ADF≌△BDE得到:S...科目:初中数学 来源:甘肃省平凉市2017-2018学年八年级(上)期中数学试卷 题型:解答题
如图,B、F、E、C四点在同一条直线上,AB=CD,AE=DF,CE=FB,判断∠B与∠C的关系,并证明.

查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学人教版上册:第24章 圆 单元测试卷 题型:单选题
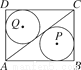
如图,矩形ABCD中,AB=4,BC=3,连接AC,⊙P和⊙Q分别是△ABC和△ADC的内切圆,则PQ的长是 ( )
A. 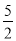 B.
B. 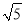 C.
C. 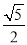 D. 2
D. 2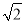
查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学人教版上册:第3章 一元一次方程 单元测试卷 题型:填空题
若-xn+1与2x2n-1是同类项,则n=____.
2. 【解析】已知2xn+1与3x2n-1是同类项,根据同类项是所含字母相同,并且相同字母的次数也相同的项,可得n+1=2n-1,解得n=2.查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学人教版上册:第3章 一元一次方程 单元测试卷 题型:单选题
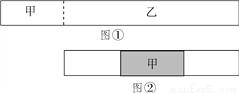
图①为一正面白色、反面灰色的长方形纸片.今沿虚线剪下分成甲、乙两长方形纸片,并将甲纸片反面朝上粘贴于乙纸片上,形成一张白、灰相间的长方形纸片,如图②所示.若图②中白色与灰色区域的面积比为8∶3,图②纸片的面积为33,则图①纸片的面积为( )
A. 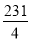 B.
B. 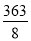 C. 42 D. 44
C. 42 D. 44
查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学人教版上册:第23章 旋转 单元测试卷 题型:解答题
如图,已知四边形ABCD,画四边形A1B1C1D1,使它与四边形ABCD关于C点中心对称.
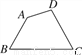
查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学人教版上册:第23章 旋转 单元测试卷 题型:填空题
如图所示,在△ABC中,∠C=90°,AC=BC=4cm.若以AC的中点O为旋转中心,将这个三角形旋转180°后,点B落在B′处,则BB′=________cm.
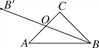
查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学人教版上册:第25章 概率初步 单元测试卷 题型:解答题
有甲、乙两个不透明的布袋,甲袋中有2个完全相同的小球,分别标有数字0和-2;乙袋中有3个完全相同的小球,分别标有数字-2,0和1,小明从甲袋中随机取出1个小球,记录标有的数字为x,再从乙袋中随机取出1个小球,记录标有的数字为y,这样确定了点Q的坐标(x,y).
(1)写出点Q所有可能的坐标;
(2)求点Q在x轴上的概率.
(1)(0,﹣2),(0,0),(0,1),(2,﹣2),(2,0),(2,1);(2) 【解析】试题分析:(1)树状图展示所有6种等可能的结果数,(2)根据点在x轴上的坐标特征确定点Q在x轴上的结果数,然后根据概率公式求解. 试题解析:(1)画树状图为: 共有6种等可能的结果数,它们为(0,﹣2),(0,0),(0,1),(2,﹣2),(2,0),(2,1); (2)点Q...查看答案和解析>>
科目:初中数学 来源:安徽省蚌埠市2017届九年级下学期中考二模数学试卷 题型:单选题
如图所示的立方体,如果把它展开,可以是下列图形中的( )
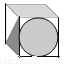
A. 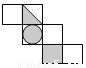 B.
B. 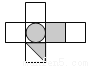 C.
C. 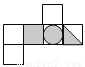 D.
D. 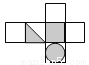
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com