
��ͼ��ʾ����A����1����2�Ĵ�С��ϵ�ǣ�������
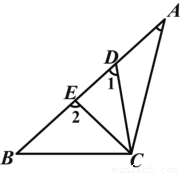
A. ��A����1����2 B. ��2����1����A C. ��A����2����1 D. ��2����A����1
B ���������������ȸ��ݡ�1�ǡ�ACD����ǣ��ʡ�1����A���ٸ��ݡ�2�ǡ�CDE����ǣ��ʡ�2����1�������ɵó����ۣ� ��𣺡������� �ߡ�1�ǡ�ACD����ǣ� ���1����A�� �ߡ�2�ǡ�CDE����ǣ� ���2����1�� ���2����1����A�� ��ѡB��
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ֣����֣������ʵ��ѧУ2017-2018ѧ����꼶���ϣ�������ѧ�Ծ� ���ͣ������
��ͼ��A��2����4����B��4����3����C��5��0�������ı���ABCO�������
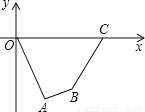
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�人�н�����2018����꼶����ĩģ����ѧ�Ծ� ���ͣ���ѡ��
һԪ���η���x2��4x+3=0�ĸ��ǣ� ��
A. ��1 B. ��3 C. 1��3 D. ��1�ͩ�3
C ��������x2��4x+3=0�� ��x��3����x��1��=0�� x��3=0��x��1=0�� x=3��1�� ��ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ѧ�˽̰���꼶�ϲ��11�µڶ������������йصĽǵ�����ʱͬ����ϰ ���ͣ������
��֪����ͼ���ڡ�ABC�У���B=��C��ADƽ����ǡ�EAC��
��֤��AD��BC��
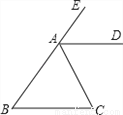
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ѧ�˽̰���꼶�ϲ��11�µڶ������������йصĽǵ�����ʱͬ����ϰ ���ͣ������
��ͼ���ڡ�ABC�У���A=45�㣬��B=60�㣬����ǡ�ACD=__�ȣ�
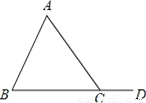
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ѧ�˽̰���꼶�ϲ��11�µڶ������������йصĽǵ�����ʱͬ����ϰ ���ͣ���ѡ��
��ͼ����֪AB��CD����EBA=45�㣬��E+��D�Ķ���Ϊ�� ��
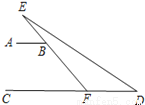
A. 30�� B. 60�� C. 90�� D. 45��
D ���������������������ƽ���ߵ����ʿɵá�CFE=45�㣬�ٸ����������ڽ�����ǵĹ�ϵ�ɵá�E+��D=��CFE�� ��AB��CD�� ���ABE=��CFE�� �ߡ�EBA=45�㣬 ���CFE=45�㣬 ���E+��D=��CFE=45�㣬 ��ѡ��D�� ����: 1.ƽ���ߵ����ʣ�2.�����ε�������ʣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ��������ɽ�羰��2018����꼶����ĩģ����ѧ�Ծ� ���ͣ������
��ͼ���ڡ�ABC�У�D�DZ�AB���е㣬DE��BC��AC�ڵ�E.��֤��AE=EC
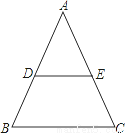
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ��������ɽ�羰��2018����꼶����ĩģ����ѧ�Ծ� ���ͣ���ѡ��
��ͼ��ʾ��ͼ���У������ɻ���ͼ��ͨ��ƽ�Ʒ����õ���ͼ���ǣ�������
A. 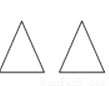 B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�����У�����У���� 2017-2018ѧ����꼶��һѧ�����в�����ѧ�Ծ� ���ͣ���ѡ��
һԪ���η���5x2��x����3�����ж�����ϵ����һ����ϵ����������ֱ���( )
A. 5����x��3 B. 5����1����3 C. 5����1��3 D. 5x2����1��3
C �������������������5x2��x����3�� 5x2��x��3��0�� ���Զ�����ϵ����һ����ϵ����������ֱ���5����1��3�� ��ѡC���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com