
 如图,在Rt△ABC中,∠C=90°,∠B=75°,将△ABC沿CD翻折,使点B落在边AC上的B′处,则BC:BD=( )
如图,在Rt△ABC中,∠C=90°,∠B=75°,将△ABC沿CD翻折,使点B落在边AC上的B′处,则BC:BD=( )| A. | $\sqrt{6}$:2 | B. | 3:2 | C. | $\sqrt{5}$:3 | D. | 5:3 |
分析 将△ABC沿CD翻折则可知CD为∠ACB的角平分线,可推导得出∠CDB=60°,从点B作BE⊥CD,设BE为x,将BD与BC的长用x表示出来则可以求出BC与BD的比.
解答 解:∵将△ABC沿CD翻折,使点B落在边AC上的B′处,∠C=90°,
∴∠ACB=∠DCB=45°,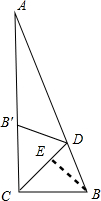 ∵∠B=75°,
∵∠B=75°,
∴∠BDC=60°,
作BE⊥CD,
设ED长为x,
∵∠BDC=60°,
∴BE=$\sqrt{3}$x,BD=2x,
∵∠DCB=45°,
∴BE=EC=$\sqrt{3}$x,
∴BC=$\sqrt{6}$x,
∴BC:BD=$\sqrt{6}$x:$\sqrt{2}$x=$\sqrt{6}$:$\sqrt{2}$.
故选:A.
点评 本题考察的是折叠的性质,解题的关键是明确CD平分∠ACB,并求出∠CDB的度数,利用特殊角得出两边的数量关系.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①是常数,②不是常数 | B. | ①是不常数,②是常数 | ||
| C. | ①、②都是常数 | D. | ①、②都不是常数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
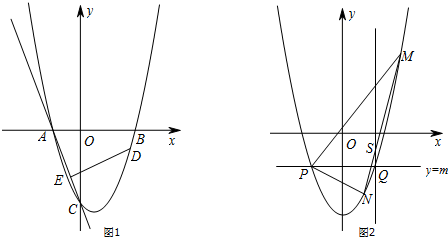
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在矩形ABCD中,点O是对角线AC上一点,以OC为半径的⊙O与CD交于点M,且∠BAC=∠DAM,请判断AM与⊙O的位置关系,并说明理由.
如图,在矩形ABCD中,点O是对角线AC上一点,以OC为半径的⊙O与CD交于点M,且∠BAC=∠DAM,请判断AM与⊙O的位置关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{28}$×$\frac{1}{2}$=$\sqrt{14}$ | B. | $\sqrt{(a-b)^{2}}$•$\frac{1}{a-b}$=1 | ||
| C. | -2x2-3x+5=(1-x)(2x+5) | D. | (-a)7÷a3=a4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com