
若△ABC三条边长为a,b,c,化简: 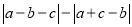 =______.
=______.
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 第6章 反比例函数 单元测试卷 题型:填空题
某市有长24000 m的新道路要铺上沥青,则铺路所需时间t(天)与铺路速度v(m/天)的函数关系式是______________.
t= (v>0) 【解析】试题解析:铺路所需要的时间t与铺路速度V之间的函数关系式是t=. 故答案为:t=.查看答案和解析>>
科目:初中数学 来源:广西北海市银海区2017-2018学年度上期教学质量监测八年级数学试卷 题型:解答题
解方程: 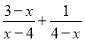 =1
=1
查看答案和解析>>
科目:初中数学 来源:江苏省姜堰区2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
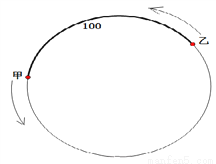
已知甲沿周长为300米的环形跑道上按逆时针方向跑步,速度为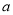 米/秒,与此同时在甲后面100米的乙也沿该环形跑道按逆时针方向跑步,速度为3米/秒.设运动时间为
米/秒,与此同时在甲后面100米的乙也沿该环形跑道按逆时针方向跑步,速度为3米/秒.设运动时间为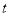 秒.
秒.
(1)若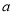 =5,求甲、乙两人第1次相遇的时间;
=5,求甲、乙两人第1次相遇的时间;
(2)当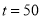 时,甲、乙两人第1次相遇.
时,甲、乙两人第1次相遇.
①求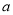 的值;
的值;
②若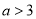 时,甲、乙两人第1次相遇前,当两人相距120米时,求
时,甲、乙两人第1次相遇前,当两人相距120米时,求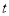 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:江苏省姜堰区2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
先化简,再求值: 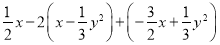 ,其中x,y满足
,其中x,y满足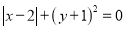
查看答案和解析>>
科目:初中数学 来源:江苏省姜堰区2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
若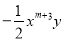 与
与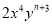 是同类项,则
是同类项,则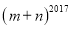 =______.
=______.
查看答案和解析>>
科目:初中数学 来源:江苏省姜堰区2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
下列图形中,把△ABC平移后,能得到△DEF的是( )
A. 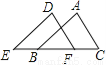 B.
B. 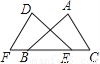
C. 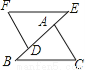 D.
D. 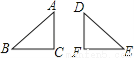
查看答案和解析>>
科目:初中数学 来源:2018人教版七年级数学下册练习:第七章达标检测卷 题型:单选题
如图(1),与图(1)中的三角形相比,图(2)中的三角形发生的变化是( )
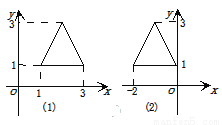
A. 向左平移3个单位长度 B. 向左平移1个单位长度
C. 向上平移3个单位长度 D. 向下平移1个单位长度
D 【解析】由图①到图②,点(1,1)平移到点(?2,1), 点(3,1)平移到点(0,1),都是向左平移3个单位, ∴图形平移规律为:向左平移3个单位。 故选A.查看答案和解析>>
科目:初中数学 来源:河北省保定市莲池区2017-2018学年上期九年级数学期末考试试卷 题型:解答题
某商品的进价为每件20元,当销售单价是25元时,每天的销售量为250件,如果调整价格,销售单价每上涨1元,每天的销售量就减少10件.
①求每天所得的销售利润w(元)与每件涨价x(元)之间的函数关系式,并写出x的取值范围.
②求销售单价为多少元时,该文具每天的销售利润最大?最大利润是多少?
③若商场要每天获得销售利润2000元,同时让利于顾客,销售单价应定为多少元?
①w=﹣10x2+200x+1250( 0≤x≤25 )②当单价为35元时,该文具每天的利润最大,最大利润为2250元③商场要每天获得销售利润2000元,销售单价应定为30元 【解析】试题分析:①根据利润=(销售单价-进价)×销售量,列出函数关系式即可; ②根据(1)式列出的函数关系式,运用配方法求最大值; ③根据利润等于2000元,列出方程求解即可. 试题解析:①w=(2...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com