
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源:河南省禹州市2017-2018学年九年级上学期期中考试数学试卷 题型:填空题
一元二次方程a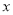 2+b
2+b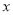 +c=0的两根是-
+c=0的两根是-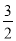 、-1,则二次函数y=a
、-1,则二次函数y=a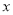 2+b
2+b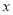 +c的图象与
+c的图象与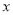 轴的两个交点间的距离为 .
轴的两个交点间的距离为 .
查看答案和解析>>
科目:初中数学 来源:江苏省徐州市区联校2017-2018学年八年级上学期期中联考数学试卷 题型:填空题
如图,已知所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大正方形的边长为5,则A,B,C,D四个小正方形的面积之和等于________ .
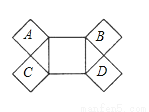
查看答案和解析>>
科目:初中数学 来源:湖南省新化县2016-2017学年度第二学期期中检测七年级数学试卷 题型:解答题
已知方程组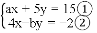 ,甲由于看错了方程①中的a,得到方程组的解为
,甲由于看错了方程①中的a,得到方程组的解为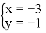 乙由于看错了方程②中的b,得到方程组的解为
乙由于看错了方程②中的b,得到方程组的解为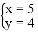 ,若按正确的a,b计算,求原方程组的解.
,若按正确的a,b计算,求原方程组的解.
查看答案和解析>>
科目:初中数学 来源:湖南省新化县2016-2017学年度第二学期期中检测七年级数学试卷 题型:填空题
已知m2+n2-6m+10n+34=0,则m+n= __________
-2 【解析】【解析】 ∵(m-3)2+(n+5)2=0,∴m-3=0,n+5=0,解得:m=3,n=-5,∴m+n=3-5=-2.故答案为:-2.查看答案和解析>>
科目:初中数学 来源:湖南省新化县2016-2017学年度第二学期期中检测七年级数学试卷 题型:单选题
如图,将正方形ABCD的一角折叠,折痕为AE,∠BAD比∠BAE大48°.设∠BAD和∠BAE的度数分别为x°,y°,那么x,y所适合的一个方程组是( )
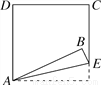
A. 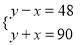 B.
B. 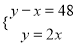 C.
C. 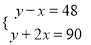 D.
D. 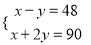
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型:解答题
在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
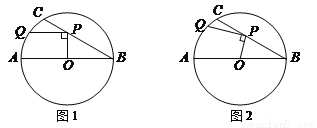
(1)如图1,当PQ∥AB时,求PQ的长度;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
(1);(2). 【解析】试题分析:(1)在Rt△OPB中,由OP=OB·tan∠ABC可求得OP=,连接OQ,在Rt△OPQ中,根据勾股定理可得PQ的长;(2)由勾股定理可知OQ为定值,所以当当OP最小时,PQ最大.根据垂线段最短可知,当OP⊥BC时OP最小,所以在Rt△OPB中,由OP=OB·sin∠ABC求得OP的长;在Rt△OPQ中,根据勾股定理求得PQ的长. 试题解析:【解析...查看答案和解析>>
科目:初中数学 来源:江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型:填空题
函数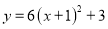 的顶点坐标是___________.
的顶点坐标是___________.
查看答案和解析>>
科目:初中数学 来源:2017年河南省中考数学三模试卷 题型:解答题
某校为了解“课程选修”的情况,对报名参加“艺术鉴赏”、“科技制作”、“数学思维”、“阅读写作”这四个选修项目的学生(每人限报一项)进行抽样调查,下面是根据收集的数据绘制的两幅不完整的统计图.
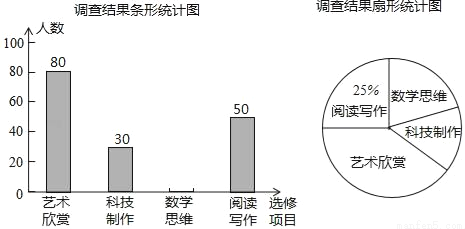
根据图中提供的信息,解答下列问题:
(1)此次共调查了 名学生,扇形统计图中,“艺术鉴赏”所对应的圆心角的度数是 度;
(2)请把这个条形统计图补充完整;
(3)现该校700名学生报名参加这四个选修项目,请你估计有多少名学生参加了“数学思维”项目.
(1)200,144(2)40人(3)该校700名学生有140名学生参加了“数学思维”项目 【解析】试题分析: (1)根据总人数=所占人数÷百分数,圆心角=360°×百分比,分别计算即可; (2)求出数学思维的人数,画出条形图即可; (3)用样本估计总体的思想思考问题即可; 解:(1)总人数=50÷25%=200人, 艺术鉴赏”所对应的圆心角的度数=360°×=144...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com