
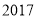 年
年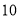 月
月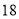 日
日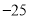 日在北京胜利召开了“中国共产党第十九次代表大会”.截止到
日在北京胜利召开了“中国共产党第十九次代表大会”.截止到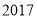 年
年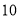 月
月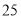 日晚
日晚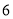 时,在百度上搜索关键词“十九大”,显示的搜索结果约为
时,在百度上搜索关键词“十九大”,显示的搜索结果约为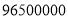 条,将
条,将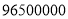 用科学记数法表示应为( ).
用科学记数法表示应为( ).
A. 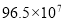 B.
B. 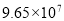 C.
C. 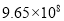 D.
D. 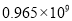
科目:初中数学 来源:江苏省南京市联合体2018届九年级上学期期末考试数学试卷 题型:解答题
商场某种商品平均每天可销售30件,每件盈利50元,为了尽快减少库存,商场决定采取适当的降价措施.经调査发现,每件商品每降价1元,商场平均每天可多售出2件.
(1)若某天该商品每件降价3元,当天可获利多少元?
(2)设每件商品降价x元,则商场日销售量增加 件,每件商品盈利 元(用含x的代数式表示);
(3)在上述情况下,每件商品降价多少元时,商场日盈利可达到2000元?
(1)若某天该商品每件降价3元,当天可获利1692元; (2)2x;50﹣x. (3)每件商品降价25元时,商场日盈利可达到2000元. 【解析】试题分析:(1)根据“盈利=单件利润×销售数量”即可得出结论; (2)根据“每件商品每降价1元,商场平均每天可多售出2件”结合每件商品降价x元,即可找出日销售量增加的件数,再根据原来没见盈利50元,即可得出降价后的每件盈利额;...查看答案和解析>>
科目:初中数学 来源:山东省东营市河口区2017-2018学年度第一学期期末考试九年级数学试卷 题型:单选题
若二次函数y=x2+mx的对称轴是x=3,则关于x的方程x2+mx=7的解为( )
A. x1=0,x2=6 B. x1=1,x2=7 C. x1=1,x2=﹣7 D. x1=﹣1,x2=7
D 【解析】试题分析:先根据二次函数y=x2+mx的对称轴是x=3求出m的值,再把m的值代入方程x2+mx=7,求出x的值即可. ∵二次函数y=x2+mx的对称轴是x=3, ∴﹣=3,解得m=﹣6, ∴关于x的方程x2+mx=7可化为x2﹣6x﹣7=0,即(x+1)(x﹣7)=0,解得x1=﹣1,x2=7.查看答案和解析>>
科目:初中数学 来源:北京大学附属中学2017-2018学年七年级上学期期中考试数学试卷 题型:填空题
在数轴上表示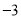 的点的距离等于
的点的距离等于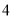 个单位长度的点所表示的数是__________.
个单位长度的点所表示的数是__________.
查看答案和解析>>
科目:初中数学 来源:北京大学附属中学2017-2018学年七年级上学期期中考试数学试卷 题型:单选题
如图,点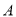 和
和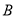 表示的数分别为
表示的数分别为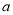 和
和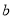 ,下列式子中,不正确的是( ).
,下列式子中,不正确的是( ).
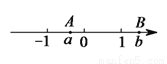
A. 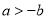 B.
B. 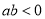 C.
C. 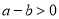 D.
D. 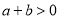
查看答案和解析>>
科目:初中数学 来源:天津市2018届九年级(上)第四周周清数学试卷 题型:解答题
已知二次函数图象的顶点是(1,2),且这个函数过点(2,3),求这个二次函数的解析式.
y=(x﹣1)2+2 【解析】试题分析:由于已知抛物线顶点坐标,则设顶点式=a(x﹣1)2+2,然后把(2,3)代入求出a即可; 试题解析:∵抛物线的顶点是(1,2), ∴设抛物线的解析式为y=a(x﹣1)2+2(a≠0). ∵抛物线过点(2,3), ∴a(2﹣1)2+2=3,解得a=1, ∴抛物线的解析式为y=(x﹣1)2+2.查看答案和解析>>
科目:初中数学 来源:天津市2018届九年级(上)第四周周清数学试卷 题型:单选题
如图所示,是二次函数y=ax2﹣bx+2的大致图象,则函数y=﹣ax+b的图象不经过( )
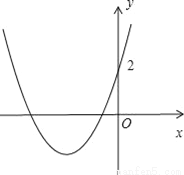
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
A 【解析】试题解析:∵二次函数y=ax2﹣bx+2的图象开口向上, ∴a>0; ∵对称轴x=﹣<0, ∴b<0; 因此﹣a<0,b<0 ∴综上所述,函数y=﹣ax+b的图象过二、三、四象限. 即函数y=﹣ax+b的图象不经过第一象限. 故选A.查看答案和解析>>
科目:初中数学 来源:广东省广州市天河区2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
如果10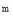 =4,10ⁿ=6,那么10
=4,10ⁿ=6,那么10 =__________.
=__________.
查看答案和解析>>
科目:初中数学 来源:湖南省武冈市2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
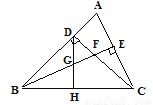
已知:如图, 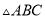 中,
中, 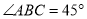 ,
, 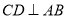 于
于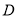 ,
, 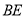 平分
平分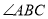 ,且
,且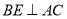 于
于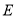 ,与
,与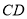 相交于点
相交于点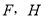 是
是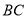 边的中点,连结
边的中点,连结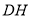 与
与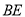 相交于点
相交于点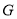 .
.
(1)求证: 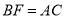 ;
;
(2)求证: 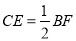 ;
;
(3)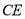 与
与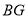 的大小关系如何?试证明你的结论.
的大小关系如何?试证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com