练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    二次函数y=x2﹣2x+6的最小值是____．

    5 【解析】试题分析：y=x2﹣2x+6=x2﹣2x+1+5 =（x﹣1）2+5， 可见，二次函数的最小值为5．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年山东省临沂市沂水县七年级（上）期中数学试卷 题型：单选题

    下列计算正确的是（　　）

    A. ﹣2（x+3y）=﹣2x+3y B. ﹣2（x+3y）=﹣2x﹣3y

    C. ﹣2（x+3y）=﹣2x+6y D. ﹣2（x+3y）=﹣2x﹣6y

    D 【解析】利用去括号法则得到?2(x+3y)=?2x?6y， 故选D

    查看答案和解析>>

    科目：初中数学 来源：江苏省丹阳市2017-2018学年八年级12月月考数学试卷 题型：解答题

    已知y=y1－y2，其中y1与x成正比例，y2与x+3成正比例，当x=－1时，y=5；当x=2时，y=8，求y与x得函数表达式．

    y=x＋6 【解析】试题分析：根据题意设 则 再根据与的取值，求出的取值即可. 试题解析： 与成正比例，设 与成正比例，设 又 ∴ 当时， 当时， 解得 所以

    查看答案和解析>>

    科目：初中数学 来源：江苏省丹阳市2017-2018学年八年级12月月考数学试卷 题型：填空题

    计算： ．

    4 【解析】 试题分析：根据立方根的意义可知===4．

    查看答案和解析>>

    科目：初中数学 来源：江苏省2018届九年级12月月考数学试卷 题型：解答题

    已知抛物线的顶点为（1，﹣4），且过点（﹣2，5）．

    （1）求抛物线解析式；

    （2）求函数值y＞0时，自变量x的取值范围．

    （1）y=x2﹣2x﹣3；（2）x＜﹣1或x＞3时，y＞0． 【解析】试题分析：（1）由于已知抛物线顶点坐标，则可设顶点式y=a（x﹣1）2﹣4，然后把（﹣2，5）代入求出a的值即可； （2）先求出抛物线与x轴的交点坐标，然后写出抛物线在x轴上方所对应的自变量的取值范围即可． 【解析】 （1）设抛物线解析式为y=a（x﹣1）2﹣4， 把（﹣2，5）代入得a•（﹣2﹣1）2...

    查看答案和解析>>

    科目：初中数学 来源：江苏省2018届九年级12月月考数学试卷 题型：填空题

    挂钟分针的长10cm，经过45分钟，它的针尖转过的弧长是 cm.

    ． 【解析】 试题分析：分针经过60分钟，转过360°，经过45分钟转过270°， 则分针的针尖转过的弧长是． 故答案是．

    查看答案和解析>>

    科目：初中数学 来源：江苏省2018届九年级12月月考数学试卷 题型：单选题

    二次函数y=x2﹣2x﹣3的图象与y轴的交点坐标是（　　）

    A. （0，﹣3） B. （1，0） C. （1，﹣4） D. （3，0）

    A 【解析】【解析】 当x=0时，y=-3，故图象与y轴的交点坐标是（0，-3）．故选A．

    查看答案和解析>>

    科目：初中数学 来源：郑州二中学区2017-2018学年上学期期中学业水平测试 八年级数学试卷 题型：解答题

    △ABC在直角坐标系内的位置如图所示．

    （1）分别写出A、B、C的坐标；

    （2）请在这个坐标系内画出△A1B1C1，使△A1B1C1与△ABC关于y轴对称，并写出B1的坐标；

    （3）请在这个坐标系内画出△A2B2C2，使△A2B2C2与△ABC关于原点对称，并写出A2的坐标．

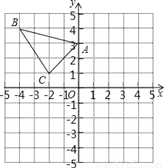
    【答案】（1）A（0，3）；B（﹣4，4）；C（﹣2，1）；（2）B1的坐标为：（4，4）；（3）A2（0，﹣3）

    【解析】试题分析：（1）根据三角形在平面直角坐标系的位置，分别写出作标点；（2）作关于y轴对称的图形见解析；（3）作关于原点对称图形见解析；

    试题解析:（1）根据平面直角坐标系可知点A,B,C的坐标为A(0,3);B(-4,4);C(-2,1)；

    （2）作图如下图:(4,4)；（3）作图如下:(0,-3).

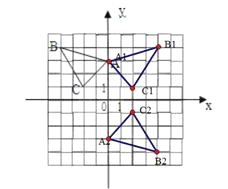
    考点：1.作图-轴对称变换2.作图-中心对称变换3.象限内点的坐标

    【题型】解答题
    【结束】
    19

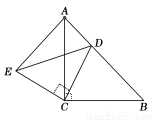
    如图，△ACB和△ECD都是等腰直角三角形，∠ACB＝∠ECD＝90°，D为AB边上一点，求证：

    （1）△ACE≌△BCD；（2）．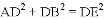

    （1）证明见解析；（2）证明见解析． 【解析】试题分析：（1）本题要判定，已知和都是等腰直角三角形，，则，，，又因为两角有一个公共的角，所以，根据得出． （2）由（1）的论证结果得出，，． 试题解析： （1）∵， ∴ ∴． ∵，， ∴． （2）∵是等腰直角三角形， ∴． ∵， ∴ ∴， ∴． 由（1）知AE=...

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级数学上册经典试卷 第21章 一元二次方程韦达定理 测试卷 题型：单选题

    已知a≥2，m2﹣2am+2=0，n2﹣2an+2=0，m≠n，则（m﹣1）2+（n﹣1）2的最小值是（　　）

    A. 6 B. 3 C. ﹣3 D. 0

    A 【解析】已知m2﹣2am+2=0，n2﹣2an+2=0，可得m，n是关于x的方程x2﹣2ax+2=0的两个根，根据根与系数的关系可得m+n=2a，mn=2，再由（m﹣1）2+（n﹣1）2=m2﹣2m+1+n2﹣2n+1=（m+n）2﹣2mn﹣2（m+n）+2=4a2﹣4﹣4a+2=4（a﹣ ）2﹣3，因a≥2，所以当a=2时，（m﹣1）2+（n﹣1）2有最小值，即（m﹣1）2+（n﹣1）...

    查看答案和解析>>

    同步练习册答案