
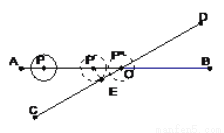
如图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在射线OA上,开始时,PO=6cm,如果⊙P以1cm/秒的速度沿由A向B的方向移动,那么当⊙P的运动时间t(秒)满足什么条件时,⊙P与直线CD相交?
科目:初中数学 来源:广东省2017届九年级上学期第二次月考数学试卷 题型:单选题
函数y=x2﹣2x+3的图象的顶点坐标是( )
A. (1,﹣4) B. (﹣1,2) C. (1,2) D. (0,3)
C 【解析】试题分析:首先将二次函数配成顶点式,然后得出顶点坐标.y=-2x+3=,则顶点坐标为(1,2)查看答案和解析>>
科目:初中数学 来源:《概率的进一步认识》单元测试2 题型:单选题
中央电视台“幸运52”栏目中的“百宝箱”互动环节,是一种竞猜游戏,游戏规则如下:在20个商标中,有5个商标牌的背面注明了一定的奖金额,其余商标的背面是一张苦脸,若翻到它就不得奖.参加这个游戏的观众有三次翻牌的机会.某观众前两次翻牌均得若干奖金,如果翻过的牌不能再翻,那么这位观众第三次翻牌获奖的概率是( )
A. 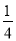 B.
B. 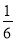 C.
C. 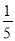 D.
D. 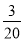
查看答案和解析>>
科目:初中数学 来源:《概率的进一步认识》单元测试2 题型:填空题
从装有5个红球和3个白球的袋中任意取4个,那么取到的“至少有1个是红球”与“没有红球”的概率分别为 和 。
1,0 【解析】 试题分析:根据必然事件和不可能事件的概率即可作出判断. 由题意得取到的“至少有1个是红球” 的概率为1,取到的“没有红球”的概率为0.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(1)练习 题型:解答题
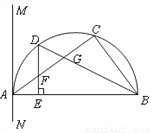
如图,△ABC内接于半圆,AB是直径,过A作直线MN,若∠MAC=∠ABC.
(1)求证:MN是半圆的切线;
(2)设D是弧AC的中点,连结BD交AC 于G,过D作DE⊥AB于E,交AC于F.求证:FD=FG.
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 21.2.1配方法(1)练习 题型:解答题
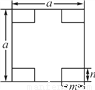
如图,在边长为a的正方形纸片的四个角都剪去一个长为m,宽为n的矩形.
(1)用含a,m,n的式子表示纸片剩余部分的面积;
(2)当m=3,n=5,且剩余部分的面积等于229时,求正方形的边长a的值.
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 21.2.1配方法(1)练习 题型:单选题
给出一种运算:对于函数y=xn,规定y′=nxn-1.例如:若函数y=x4,则有y′=4x3.已知函数y=x3,则方程y′=12的解是( )
A. x1=4,x2=-4 B. x1=2,x2=-2 C. x1=x2=0 D. x1=2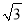 ,x2=-2
,x2=-2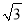
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 23.3课题学习图案设计 测试 题型:填空题
基本图案在轴对称、平移、旋转变化的过程中,图形的______和______都保持不变.
形状, 大小. 【解析】轴对称、平移、旋转变化都是全等变化,所以在变化的过程中,图形的形状和大小不变,只是位置在变化. 故答案为(1)形状;(2)大小.查看答案和解析>>
科目:初中数学 来源:《概率的进一步认识》单元测试4 题型:解答题
一个不透明的口袋里装有红、黄、绿三种颜色的球(除颜色不同外其余都相同),其中红球有2个,黄球有1个,从中任意捧出1球是红球的概率为
(1)试求袋中绿球的个数;

(2)第1次从袋中任意摸出l球(不放回),第2次再任意摸出1球,请你用画树状图或列表格的方法,求两次都摸到红球的概率.
(1)(2) 【解析】试题分析:(1)此题的求解方法是:借助于方程求解;(2)根据简单事件的概率求法解答即可;(3)此题需要两步完成,所以采用树状图或者列表法都比较简单. 试题解析::(1)设绿球的个数为x.由题意,得:,解得x=1,经检验x=1是所列方程的根,所以绿球有1个;(2)P(任意摸出一个球是黄球)=,(3)根据题意,画树状图: 由图知共有12种等可能的结果,即(红1,...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com