
��һ����30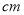 ����˿�������Σ�����ÿһ����˿����һ�������Σ�Ҫʹ�����������ε����֮�͵���86
����˿�������Σ�����ÿһ����˿����һ�������Σ�Ҫʹ�����������ε����֮�͵���86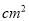 ����������һ�������ε��ܳ�Ϊ
����������һ�������ε��ܳ�Ϊ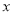 ������������з���Ϊ��������
������������з���Ϊ��������
A. 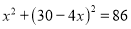 B.
B. 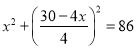
C. 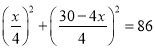 D.
D. 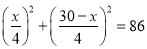
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�����ɹ�2017-2018ѧ�����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
���и�������������ȵ���( )
A. 23��32 B. ����2��4�멁24 C. ����2��3�멁23 D. 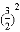 ��
��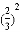
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2018����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
��������y=ax2+bx+c�Ķ�����A��2��1�����Ҿ�����B��1��0�����������ߵĺ�����ϵʽΪ__________________.
y = ������������������������ߵĽ���ʽΪy=a��x-2��2+1������B��1��0���������ʽ�������a��ֵ���Ӷ��õ����κ�������ʽ�� ����������������ߵĽ���ʽΪy=a��x-2��2+1�� ��B��1��0������y=a��x-2��2+1�ã� a=-1�� ��������ʽΪy=-��x-2��2+1�� չ����y=-x2+4x-3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ĵ�����ѧԺ����ڶ������ѧУ2018����꼶��ѧ�ڵڶ����¿���ѧ�Ծ� ���ͣ������
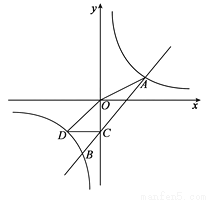
��ͼ��һ�κ���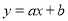 �뷴��������
�뷴��������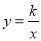 ��ͼ����A��B���㣬��A����Ϊ
��ͼ����A��B���㣬��A����Ϊ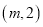 ����B����Ϊ
����B����Ϊ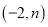 ��OA��x��������нǵ�����ֵΪ
��OA��x��������нǵ�����ֵΪ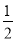 ��ֱ��AB��y���ڵ�C����C��y��Ĵ��ߣ�������������ͼ���ڵ�D������OD��BD��
��ֱ��AB��y���ڵ�C����C��y��Ĵ��ߣ�������������ͼ���ڵ�D������OD��BD��
��1����һ�κ����뷴���������Ľ���ʽ��
��2������BD�����∆BDC���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ĵ�����ѧԺ����ڶ������ѧУ2018����꼶��ѧ�ڵڶ����¿���ѧ�Ծ� ���ͣ������
ijУ���д����˶��ᣬ��Ҫ�ڳ����꼶ѡȡһ��־Ը�ߣ�������1���ࡢ������2���ࡢ������3�������2��ͬѧ�����μӣ��ִ���6��ͬѧ�����ѡȡһ������ѡ�е�����ͬѧǡ�����Գ�����3����ĸ�����___________��
�����������������������6��ͬѧ�У���2�����Գ�����3���࣬ �౻ѡ�е�����ͬѧǡ���dz�����3����ͬѧ�ĸ����ǣ��� �ʴ�Ϊ�� ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ĵ�����ѧԺ����ڶ������ѧУ2018����꼶��ѧ�ڵڶ����¿���ѧ�Ծ� ���ͣ���ѡ��
�Ĵ�����Ұ�÷��ij��֣�ij����Ϊ���Ƹõ�Ұ�õ�ֻ�����Ȳ�30ֻҰ�ø����Ƿֱ����ϱ�־��Ȼ��Żأ����б�־��Ұ����ȫ�����Ұ��Ⱥ�ڶ��β�100ֻҰ�ã���������2ֻ�б�־���Ӷ����Ƹõ�����Ұ�ã�������
A. 800ֻ B. 1000ֻ C. 1200ֻ D. 1500ֻ
D �������������������100ֻҰ�ã���������2ֻ�б�־��˵���б�־��ռ�������б�־�Ĺ���30ֻ�����Ըõ�����Ұ�ã�30�£�1500��ֻ���� ��ѡD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�꼪��ʡ�п���ѧ��ģ�Ծ� ���ͣ������
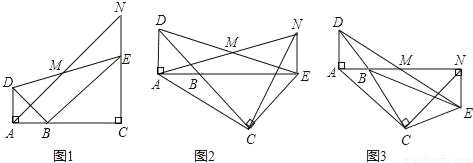
��ͼ����֪��BAD�͡�BCE��Ϊ����ֱ�������Σ���BAD=��BCE=90�㣬��MΪDE���е㣬����E��ADƽ�е�ֱ�߽�����AM�ڵ�N��
��1����A��B��C������ͬһֱ����ʱ����ͼ1����ֱ��д���߶�AD��NE��������ϵΪ�� ����
��2����ͼ1�еġ�BCE�Ƶ�B��ת����A��B��E������ͬһֱ����ʱ����ͼ2�����жϡ�ACN��ʲô���������β�˵�����ɣ�
��3����ͼ1�С�BCE�Ƶ�B��ת��ͼ3λ�ã���ʱA��B��M������ͬһֱ���ϣ���AC=3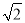 ��AD=1�����ı���ACEN�����Ϊ�� ����
��AD=1�����ı���ACEN�����Ϊ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�꼪��ʡ�п���ѧ��ģ�Ծ� ���ͣ���ѡ��
�����¼�˼ס��ҡ����������������˶�Ա�������ѡ�����ɼ���ƽ�����뷽�
�� | �� | �� | �� | |
ƽ������cm�� | 180 | 185 | 185 | 180 |
���� | 3.6 | 3.6 | 7.4 | 8.1 |
���ݱ������ݣ�Ҫ����ѡ��һ���ɼ����ҷ����ȶ����˶�Ա�μӱ�����Ӧ��ѡ������
A. �� B. �� C. �� D. ��
A ��������������������ݱ����֪����ƽ������֪�ס����ɼ��Ϻã��ɷ����֪�ס��ҳɼ����ȶ�����˿�֪Ӧѡ��ײμӱ���. ��ѡ��A�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������ʡ2017-2018ѧ�����ѧ���˽̰����꼶��ѧ�ϲ���ĩ��ϰ��ϰ�� ���ͣ������
�涨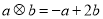 ����
����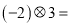 __________��
__________��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com