练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    计算：

    （1）（﹣61）﹣（﹣71）﹣|﹣8|．

    （2）3﹣[（﹣3）﹣（+12）]．

    （3）2.75﹣（﹣3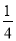）﹣（+0.5）+（﹣7）．

    （1）2；（2）18；（3）﹣2． 【解析】试题分析：（1）先计算绝对值和化简，再计算加减法即可求解先化简，再计算加减法即可求解； （2）先算小括号，再算括号外面的减法； （3）先化简，再计算同分母分数即可求解． 试题解析：（1）（﹣61）﹣（﹣71）﹣|﹣8| =﹣61+71﹣8 =﹣69+71 =2． （2）3﹣[（﹣3）﹣（+12）] =...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

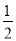    科目：初中数学 来源：河北省保定市莲池区2017-2018学年上期九年级数学期末考试试卷 题型：解答题

    如图，在平面直角坐标系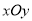 中，函数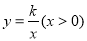的图象与直线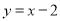交于点A(3,m).

    （1）求k、m的值；

    （2）已知点P(n，n)(n>0)，过点P作平行于轴的直线，交直线y=x-2于点M，过点P作平行于y轴的直线，交函数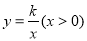 的图象于点N.

    ①当n=1时，判断线段PM与PN的数量关系，并说明理由；

    ②若PN≥PM，结合函数的图象，直接写出n的取值范围.

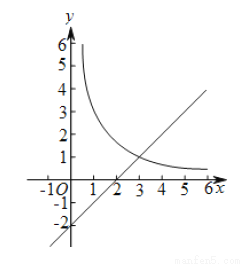
    (1) k的值为3，m的值为1；（2）00）的图象与直线y=x-2交于点A(3，m) ∴m=3-2=1，把A（3，1）代入 得，k=3×1=3，即k的值为3，m的值...

    查看答案和解析>>

    科目：初中数学 来源：广西合浦县2017年秋季学期教学质量监测九年级数学试卷 题型：单选题

    Rt△ABC中，∠C=90°，a=4，b=3，则cosA的值是（ ）

    A. B. C. D.

    A 【解析】试题分析：本体主要考查的就是三角函数的求法，根据勾股定理可得：c=5，则根据三角函数的计算法则可得：cosA==

    查看答案和解析>>

    科目：初中数学 来源：山东省滨州市惠民县2018届九年级上学期期末数学试卷 题型：单选题

    如图,若果∠1＝∠2，那么添加下列任何一个条件：（1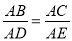），（2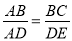），（3）∠B＝∠D，（4）∠C＝∠AED， 其中能判定△ABC∽△ADE的个数为

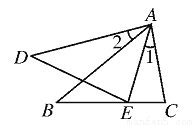
    A. 1 B. 2 C. 3 D. 4

    C 【解析】∵∠1＝∠2， ∴∠1+∠BAE=∠2+∠BAE，即∠DAE=∠BAC， ∴（1）当添加条件“”时，可由“两边对应成比例，且夹角相等的两个三角形相似”证得：△ABC∽△ADE； （2）当添加条件“”时，不能证明：△ABC∽△ADE； （3）当添加条件“∠B＝∠D”时，可由“有两个角对应相等的两个三角形相似”证得：△ABC∽△ADE； （4）当添加条件...

    查看答案和解析>>

    科目：初中数学 来源：山东省滨州市惠民县2018届九年级上学期期末数学试卷 题型：单选题

    若关于x的一元二次方程（m-1）x2+5x+m2-3m+2=0的一个根是0，则m的值是

    A. 1 B. 2 C. 1或2 D. 无解

    B 【解析】∵关于x的一元二次方程（m-1）x2+5x+m2-3m+2=0的一个根是0， ∴ ，解得： . 故答案为：2.

    查看答案和解析>>

    科目：初中数学 来源：湖南省雨花新华都学校2017-2018学年七年级（上）第一次月考数学试卷 题型：填空题

    定义“*”是一种运算符号，规定a*b=5a+4b+2015，则（﹣4）*5的值为_____．

    2015 【解析】利用已知的新定义计算，即可得到（﹣4）*5=﹣20+20+2015=2015， 故答案为：2015

    查看答案和解析>>

    科目：初中数学 来源：湖南省雨花新华都学校2017-2018学年七年级（上）第一次月考数学试卷 题型：单选题

    采摘杨梅时，每筐杨梅以5kg为基准，超过的千克数记为正数，不足的千克数记为负数，记录数据如图所示，则这4筐杨梅的总质量是（　　）

    A. 19.7kg B. 19.9kg C. 20.1kg D. 20.3kg

    C 【解析】根据有理数的加法，可得：（﹣0.1﹣0.3+0.2+0.3）+5×4=20.1（千克），即4筐杨梅的总质量是20.1千克． 故选：C．

    查看答案和解析>>

    科目：初中数学 来源：广东省潮州市潮安区2017-2018学年七年级上学期期末教学质量检测数学试卷 题型：解答题

    当a=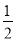时，求10-(1-a)-(1-a-a2)+(1+a-a2-a3) 的值.

    【解析】试题分析：先去括号，然后合并同类项，最后代入数值进行计算即可得. 试题解析：原式=10-1+a-1+a+a2+1+a-a2-a3=9+3a-a3 ， 当a=时，原式=9+-=.

    查看答案和解析>>

    科目：初中数学 来源：陕西省延安市大学区校际联盟2017-2018学年七年级上学期期末考试数学试卷 题型：解答题

    如图①，已知线段AB=12cm，点C为AB上的一个动点，点D、E分别是AC和BC的中点．

    （1）若AC=4cm，求DE的长；

    （2）试利用“字母代替数”的方法，说明不论AC取何值（不超过12cm），DE的长不变；

    （3）知识迁移：如图②，已知∠AOB=120°，过角的内部任一点C画射线OC，若OD、OE分别平分∠AOC和∠BOC，试说明∠DOE的度数与射线OC的位置无关．

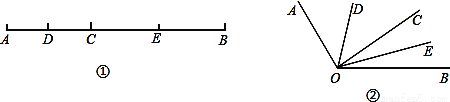
    （1）DE=6cm；（2）见解析；（3）见解析. 【解析】试题分析：（1）由AC=4cm，AB=12cm，即可推出BC=8cm，然后根据点D、E分别是AC和BC的中点，即可推出AD=DC，BE=EC，由此即可得到DE的长度； （2）设AC=acm，然后通过点D、E分别是AC和BC的中点，即可推出DE=CD+CE= (AC+BC)= AB，由此即可得到结论； （3）由若OD、OE分...

    查看答案和解析>>

    同步练习册答案