
如图,在平面直角坐标系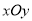 中,函数
中,函数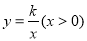 的图象与直线
的图象与直线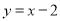 交于点A(3,m).
交于点A(3,m).
(1)求k、m的值;
(2)已知点P(n,n)(n>0),过点P作平行于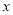 轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数
轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数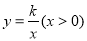 的图象于点N.
的图象于点N.
①当n=1时,判断线段PM与PN的数量关系,并说明理由;
②若PN≥PM,结合函数的图象,直接写出n的取值范围.
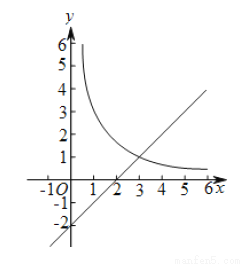
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源:江苏省姜堰区2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
将一副三角板如图放置,若∠AOD=30°,则∠BOC=______.
查看答案和解析>>
科目:初中数学 来源:2018届中考数学一轮复习单元检测:第2讲 整式与因式分解 题型:单选题
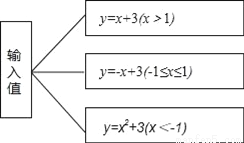
根据如图的程序,计算当输入值x=﹣2时,输出结果y为( )
A. 1 B. 5 C. 7 D. 以上都有可能
C 【解析】先由x=﹣2≤﹣1,确定x与y的关系式为y=x2+3,然后代值计算即可. 【解析】 ∵x=﹣2≤﹣1, ∴y=x2+3=(﹣2)2+3=7, 故选C.查看答案和解析>>
科目:初中数学 来源:广西合浦县2017年秋季学期教学质量监测八年级数学试卷 题型:单选题
在一个不透明的口袋中装有4个红球和若干个白球,它们除颜色外其他相同.通过多次摸球试验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有( )
A. 16个 B. 15个 C. 13个 D. 12个
D 【解析】试题分析:由摸到红球的频率稳定在25%附近得出口袋中得到红色球的概率,进而求出白球个数即可. 【解析】 设白球个数为:x个, ∵摸到红色球的频率稳定在25%左右, ∴口袋中得到红色球的概率为25%, ∴=, 解得:x=12, 故白球的个数为12个. 故选:D.查看答案和解析>>
科目:初中数学 来源:广西合浦县2017年秋季学期教学质量监测八年级数学试卷 题型:单选题
下列命题中,是真命题的是( )
①面积相等的两个直角三角形全等;
②对角线互相垂直的四边形是正方形;
③将抛物线 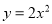 向左平移4个单位,再向上平移1个单位可得到抛物线
向左平移4个单位,再向上平移1个单位可得到抛物线 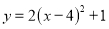 ;
;
④两圆的半径R、r分别是方程x2-3x+2=0 的两根,且圆心距d=3, 则两圆外切.
A. ① B. ② C. ③ D. ④
D 【解析】试题解析:①面积相等的两个直角三角形不一定全等,原命题是假命题; ②对角线互相垂直的四边形不一定是正方形,原命题是假命题; ③将抛物线y=2x2向左平移4个单位,再向上平移1个单位可得到抛物线y=2(x+4)2+1,原命题是假命题; ④两圆的半径R、r分别是方程x2-3x+2=0的两根,且圆心距d=3,则两圆外切,是真命题; 故选D.查看答案和解析>>
科目:初中数学 来源:河北省保定市莲池区2017-2018学年上期九年级数学期末考试试卷 题型:填空题
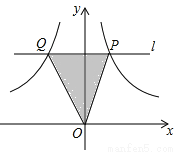
如图,在平面直角坐标系中,直线l∥x轴,且直线l分别与反比例函数y=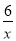 (x>0)和y=-
(x>0)和y=-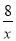 (x<0)的图象交于点P、Q,连结PO、QO,则△POQ的面积为 .
(x<0)的图象交于点P、Q,连结PO、QO,则△POQ的面积为 .
查看答案和解析>>
科目:初中数学 来源:河北省保定市莲池区2017-2018学年上期九年级数学期末考试试卷 题型:单选题
中国“一带一路”战略给沿线国家和地区带来很大的经济效益,沿线某地区居民2016年年收入300美元,预计2018年年收入将达到1500美元,设2016年到2018年该地区居民年人均收入平均增长率为x,可列方程为( )
A. 300(1+x)2=1500 B. 300(1+2x)=1500
C. 300(1+x2)=1500 D. 300+2x=1500
A 【解析】试题解析:设2016年到2018年该地区居民年人均收入平均增长率为x, 那么根据题意得2018年年收入为:300(1+x)2, 列出方程为:300(1+x)2=1500. 故选A.查看答案和解析>>
科目:初中数学 来源:广西合浦县2017年秋季学期教学质量监测九年级数学试卷 题型:填空题
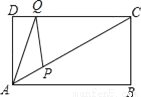
如图,矩形ABCD中,AD=3,∠CAB=30°,点P是线段AC上的动点,点Q是线段CD上的动点,则AQ+QP的最小值是_____.
查看答案和解析>>
科目:初中数学 来源:湖南省雨花新华都学校2017-2018学年七年级(上)第一次月考数学试卷 题型:解答题
计算:
(1)(﹣61)﹣(﹣71)﹣|﹣8|.
(2)3﹣[(﹣3)﹣(+12)].
(3)2.75﹣(﹣3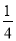 )﹣(+0.5)+(﹣7
)﹣(+0.5)+(﹣7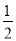 ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com