
在△ABC中∠C=90°,D,E为AC上的两点,且AE=DE,BD平分∠EBC,则下列说法不正确的是( )
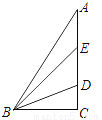
A. BC是△ABE的高 B. BE是△ABD的中线
C. BD是△EBC的角平分线 D. ∠ABE=∠EBD=∠DBC
D 【解析】解:A.BC是△ABE的高,正确,不符合题意; B.BE是△ABD的中线,正确,不符合题意; C.BD是△EBC的角平分线,正确,不符合题意; D.∵BD是△EBC的角平分线,∴∠EBD=∠DBC,∵BE是中线,∴∠ABE≠∠EBD,∴∠ABE=∠EBD=∠DBC不正确,符合题意. 故选D. 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源:湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型:解答题
阅读下面材料,并解决问题:问 题:如图1,等边△ABC内有一点P,若点P到顶点A,B,C的距离分别为6,8,10,求∠APB的度数?
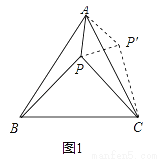
分 析:由于PA,PB,PC不在同一个三角形中,为了解决本题我们可以将△ABP绕顶点A旋转到△ACP′处,此时△ACP′和△ABP全等,这样,就可以利用全等三角形知识,将三条线段的长度转化到同一个三角形中从而求出∠APB的度数.
(1)请你按上述方法求出图1中∠APB的度数;
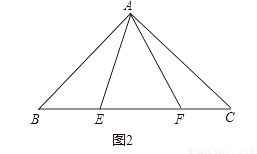
(2)请你利用第(1)题的解答思想方法,解答下面问题:如图2,已知△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点,且∠EAF=45°,求证:EF2=BE2+FC2 .
(1)150°;(2)证明见解析. 【解析】试题分析:(1)根据旋转变换前后的两个三角形全等,全等三角形对应边相等,全等三角形对应角相等以及等边三角形的判定和勾股定理逆定理解答; (2)把△ABE绕点A逆时针旋转90°得到△ACE′,根据旋转的性质可得AE′=AE,CE′=CE,∠CAE′=∠BAE,∠ACE′=∠B,∠EAE′=90°,再求出∠E′AF=45°,从而得到∠EAF=∠E...查看答案和解析>>
科目:初中数学 来源:2017-2018苏科版南京栖霞区七年级数学上册12月份月考试卷有答案 题型:解答题
列出算式
(1)已知一个角的补角是这个角的余角的3倍少10°,求这个角的度数.
(2)一个角的余角比它的补角 还多1°,求这个角的度数.
还多1°,求这个角的度数.
查看答案和解析>>
科目:初中数学 来源:2017-2018苏科版南京栖霞区七年级数学上册12月份月考试卷有答案 题型:单选题
下列说法正确的个数是( )
①同角或等角的补角相等;
②两个锐角与一个钝角的和一定大于平角;
③两锐角之和一定大于直角;
④两个钝角的和一定大于平角。
A. 1 B. 2 C. 3 D. 0
B 【解析】①同角或等角的补角相等,正确; ②两个锐角与一个钝角的和一定大于平角,错误,如15°+20°+100°<180°; ③两锐角之和一定大于直角,错误,如30°+40°<90°; ④两个钝角的和一定大于平角,正确。 故选B.查看答案和解析>>
科目:初中数学 来源:湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型:解答题
如图所示的一块地,已知AD=4m,CD=3m,∠ADC=90°,AB=13m,BC=12m,求这块地的面积.
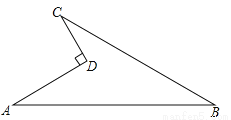
查看答案和解析>>
科目:初中数学 来源:湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型:单选题
某农户买黄金瓜,第一天上午买了45斤,价格为每斤x元,下午他又买了35斤,价格为每斤y元.第二天他以每斤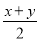 元的价格卖完了80斤,结果同第一天比发现自己亏了.其原因是( )
元的价格卖完了80斤,结果同第一天比发现自己亏了.其原因是( )
A. x<y B. x>y C. x≤y D. x≥y
B 【解析】【解析】 根据题意,可得:买黄瓜每斤的平均价>卖黄瓜每斤的平均价,∴(45x+35y)÷(45+35)>,∴(45x+35y)÷80>,∴(45x+35y)÷80×80>×80,∴45x+35y>40x+40y,整理,可得:x>y.故选B.查看答案和解析>>
科目:初中数学 来源:湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型:填空题
使不等式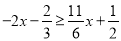 成立的最大的整数解是________.
成立的最大的整数解是________.
查看答案和解析>>
科目:初中数学 来源:2017年山东省中考数学二模试卷 题型:单选题
已知AC⊥BC于C,BC=a,CA=b,AB=c,下列选项中⊙O的半径为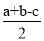 的是( )
的是( )
A. 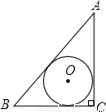 B.
B. 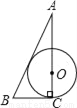 C.
C. 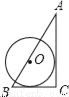 D.
D. 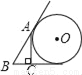
查看答案和解析>>
科目:初中数学 来源:福建省建瓯市2018届九年级数学上册期末测试卷 题型:解答题
已知直线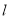 与⊙O,AB是⊙O的直径,AD⊥
与⊙O,AB是⊙O的直径,AD⊥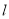 于点D.
于点D.
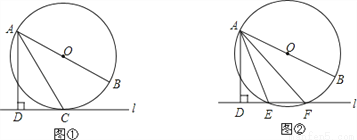
(1)如图①,当直线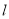 与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;
与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;
(2)如图②,当直线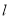 与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小.
与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com