练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下列说法正确的个数是（ ）

    ①同角或等角的补角相等；

    ②两个锐角与一个钝角的和一定大于平角；

    ③两锐角之和一定大于直角；

    ④两个钝角的和一定大于平角。

    A. 1 B. 2 C. 3 D. 0

    B 【解析】①同角或等角的补角相等，正确； ②两个锐角与一个钝角的和一定大于平角，错误，如15°+20°+100°＜180°； ③两锐角之和一定大于直角，错误，如30°+40°＜90°； ④两个钝角的和一定大于平角，正确。 故选B.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型：填空题

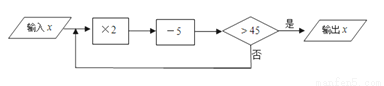
    按如图所示的程序进行运算时，发现输入的x恰好经过3次运算输出，则输入的整数x的值是________ ．

     

    11或12或13或14或15． 【解析】试题分析：第一次的结果为：2x-5，没有输出，则2x-545，解得：x25；第二次的结果为：2（2x-5）-4=4x-15，没有输出，则4x-1545，解得：x15；第三次的结果为：2（4x-15）-5=8x-35，输出，则8x-3545，解得：x10，综上可得：，则x的最小整数值为11.

    查看答案和解析>>

    科目：初中数学 来源：辽宁省2017-2018学年八年级上学期期末模拟数学试卷 题型：单选题

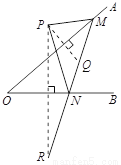
    如图，点P是∠AOB外的一点，点M，N分别是∠AOB两边上的点，点P关于OA的对称点Q恰好落在线段MN上，点P关于OB的对称点R落在MN的延长线上．若PM＝2．5cm，PN＝3cm，MN＝4cm，则线段QR的长为（ ）

    A. 4．5cm B. 5．5cm C. 6．5cm D. 7cm

    A 【解析】试题分析：利用轴对称图形的性质得出PM=MQ，PN=NR，进而利用PM=2．5cm，PN=3cm，MN=4cm，得出NQ=MN-MQ=4-2．5=1．5（cm），即可得出QR的长RN+NQ=3+1．5=4．5（cm）． 故选：A．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018苏科版南京栖霞区七年级数学上册12月份月考试卷有答案 题型：填空题

    已知直线a，b，c在同一平面内，给出下列说法：①如果a⊥b，b⊥c，那么a∥c；②如果a∥b，b∥c，那么a∥c；③如果a∥b，b⊥c，那么a⊥c；④如果a与b相交，b与c相交，那么a与c相交．在上述四种说法中，正确的有__________个．

    3 【解析】①如果a⊥b，b⊥c，那么a∥c，正确； ②如果a∥b，b∥c，那么a∥c，正确； ③如果a∥b，b⊥c，那么a⊥c，正确； ④如果a与b相交，b与c相交，那么a与c相交，错误，a与c有可能平行． 故答案为3.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018苏科版南京栖霞区七年级数学上册12月份月考试卷有答案 题型：填空题

    如果一个几何体的三个视图之一是三角形，这个几何体可能是_______、_______、_______．（写出3个即可）．

    三棱柱、 三棱锥、 圆锥 【解析】如果俯视图是三角形，则这个几何体可能是三棱锥，如果主视图或左视图是三角形，则这个几何体可能是三棱锥或圆锥. 故答案为 (1). 三棱柱、 (2). 三棱锥、 (3). 圆锥

    查看答案和解析>>

    科目：初中数学 来源：2017-2018苏科版南京栖霞区七年级数学上册12月份月考试卷有答案 题型：单选题

    下列图形中，沿其一边快速旋转能得到圆柱的是 ( )

    A. 直角三角形 B. 梯形 C. 长方形 D. 等腰三角形

    C 【解析】因为圆柱的上底圆和下底圆分别是两个半径相等的圆，所以是梯形. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型：单选题

    在△ABC中∠C=90°，D，E为AC上的两点，且AE=DE，BD平分∠EBC，则下列说法不正确的是（  ）

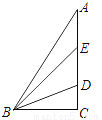
    A. BC是△ABE的高  B. BE是△ABD的中线

    C. BD是△EBC的角平分线  D. ∠ABE=∠EBD=∠DBC

    D 【解析】解：A．BC是△ABE的高，正确，不符合题意； B．BE是△ABD的中线，正确，不符合题意； C．BD是△EBC的角平分线，正确，不符合题意； D．∵BD是△EBC的角平分线，∴∠EBD=∠DBC，∵BE是中线，∴∠ABE≠∠EBD，∴∠ABE=∠EBD=∠DBC不正确，符合题意． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：2017年山东省中考数学二模试卷 题型：解答题

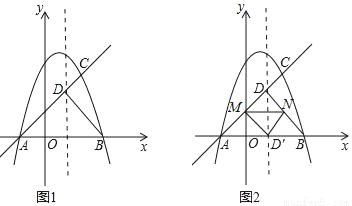
    如图1，已知抛物线y=﹣x2+bx+c与x轴交于A（﹣1，0），B两点，（点A在点B的左侧），与直线AC交于点C（2，3），直线AC与抛物线的对称轴l相交于点D，连接BD．

    （1）求抛物线的函数表达式，并求出点D的坐标；

    （2）如图2，若点M、N同时从点D出发，均以每秒1个单位长度的速度分别沿DA、DB运动，连接MN，将△DMN沿MN翻折，得到△D′MN，判断四边形DMD′N的形状，并说明理由，当运动时间t为何值时，点D′恰好落在x轴上？

    （3）在平面内，是否存在点P（异于A点），使得以P、B、D为顶点的三角形与△ABD相似（全等除外）？若存在，请直接写出点P的坐标，若不存在，请说明理由．

    （1）抛物线的解析式为y=﹣x2+2x+3，点D的坐标为（1，2）．（2）四边形DMD′N是正方形，理由见解析,经过s时，点D恰好落在x轴上的D′处．（3）存在，点P的坐标为（1，0）或（2，3）． 【解析】试题分析：（1）先利用待定系数法求得抛物线和直线的解析式，从而得出对称轴与直线的交点； （2）由抛物线解析式求得点A、B坐标，结合点D坐标可知△ABD为等腰直角三角形，即∠DAB=...

    查看答案和解析>>

    科目：初中数学 来源：2017年江苏省苏州市中考数学三模试卷 题型：填空题

    分解因式：2xy﹣6x2=_____．

    2x（y﹣3x） 【解析】试题解析：原式 故答案为：

    查看答案和解析>>

    同步练习册答案