
机械厂加工车间有85名工人,平均每人每天加工大齿轮16个或小齿轮10个,已知2个大齿轮与3个小齿轮配成一套,则应安排 ________名工人加工大齿轮,才能使每天加工的大小齿轮刚好配套.
25 【解析】【解析】 设需安排x名工人加工大齿轮,安排y名工人加工小齿轮,由题意得: ,解得: .即安排25名工人加工大齿轮,才能使每天加工的大小齿轮刚好配套. 故答案为:25. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:人教版初中数学七年级下册第六章《实数》同步练习 题型:解答题
计算: 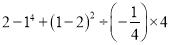 .
.
查看答案和解析>>
科目:初中数学 来源:河南省南阳市镇平县2018届九年级(上)期中数学试卷(word版含答案解析) 题型:解答题
如图,在矩形ABCD中,已知AB=24,BC=12,点E沿BC边从点B开始向点C以每秒2个单位长度的速度运动;点F沿CD边从点C开始向点D以每秒4个单位长度的速度运动,如果E、F同时出发,用t(0≤t≤6)秒表示运动的时间,当t为何值时,以点E、C、F为顶点的三角形与△ACD相似?
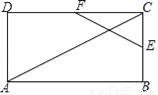
查看答案和解析>>
科目:初中数学 来源:河南省南阳市镇平县2018届九年级(上)期中数学试卷(word版含答案解析) 题型:单选题
下列式子为最简二次根式的是( )
A. 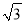 B.
B. 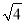 C.
C. 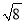 D.
D. 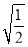
查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学人教版上册:全册综合测试卷 题型:解答题
如图,BD平分∠ABC,BE分∠ABC分2:5两部分,∠DBE=21°,求∠ABC的度数.
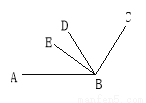
查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学人教版上册:全册综合测试卷 题型:填空题
如图,已知∠AOB=90°,若∠1=35°,则∠2的度数是____.
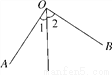
查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学人教版上册:全册综合测试卷 题型:单选题
在三角形ABC中,AB=8,AC=9,BC=10.P0为BC边上的一点,在边AC上取点P1,使得CP1=CP0,在边AB上取点P2,使得AP2=AP1,在边BC上取点P3,使得BP3=BP2,若P0P3=1,则CP0的长度为( )
A. 4 B. 6 C. 4或5 D. 5或6
D 【解析】设CP0的长度为x,则CP1=CP0=x,AP2=AP1=9-x,BP3=BP2=x-1,BP0=10-x, ∵P0P3=1, ∴|10-x-(x-1)|=1, 11-2x=±1, 解得x=5或6. 故选D.查看答案和解析>>
科目:初中数学 来源:人教版八年级下册数学 第17章 勾股定理 单元检测卷 题型:解答题
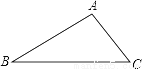
已知:如图,在△ABC中,∠B=30°,∠C=45°,AC=2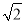 ,
,
求:(1)AB的长为________;
(2)S△ABC=________.
查看答案和解析>>
科目:初中数学 来源:广东省汕头市龙湖区2017-2018学年七年级上学期期末质量检测数学试卷 题型:单选题
如图,一副三角尺按不同的位置摆放,其中∠α=∠β的图形个数是( )

A. 1 B. 2 C. 3 D. 4
C 【解析】 图1中,∵∠α+∠β=90°,∠β=45°,∴∠α=45°,∴∠α=∠β; 图2中,∵∠α=180°-45°=135°,∠β=180°-45°=135°,∴∠α=∠β; 图3中,∠β=90°-30°=60°,∠α=180°-60°=120°,∴∠α≠∠β; 图4 中,∵∠α+∠ABC=90°,∠ABC+∠β=90°,∴∠α=∠β; 故选C. ...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com