
有一半径为1m的圆形铁片,要从中剪出一个最大的圆心角为90°的扇形ABC,用来围成一个圆锥,该圆锥底面圆的半径是_____.
科目:初中数学 来源:浙江杭州拱墅区文澜中学2017-2018学年七年级上学期中考试数学试卷(含解析) 题型:填空题
我国在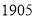 年清朝学堂的课本中用“
年清朝学堂的课本中用“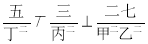 ”来表示相当于“
”来表示相当于“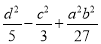 ”,那么“
”,那么“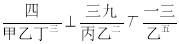 ”表示相当于__________.
”表示相当于__________.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级人教版数学试卷(C卷) 题型:解答题
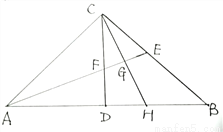
如图,在△ABC中,∠ACB=90°,AC=BC,△ABC的高CD与角平分线AE相交点F,过点C作CH⊥AE于G,交AB于H.
(1)求∠BCH的度数;
(2)求证:CE=BH.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级人教版数学试卷(C卷) 题型:单选题
如图,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm速度向点A运动,点Q从点A同时出发以每秒2cm速度向点C运动,其中一个动点到达端点,另一个动点也随之停止,当△APQ是以PQ为底的等腰三角形时,运动的时间是( )秒
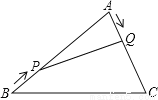
A. 2.5 B. 3 C. 3.5 D. 4
D 【解析】【解析】 设运动的时间为x,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm的速度向点A运动,点Q从点A同时出发以每秒2cm的速度向点C运动,当△APQ是等腰三角形时,AP=AQ,AP=20﹣3x,AQ=2x,即20﹣3x=2x,解得x=4.故选D.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级人教版数学试卷(C卷) 题型:单选题
剪纸是中国的民间艺术,剪纸的方法很多,图中是一种剪纸方法的图示(先将纸折叠,然后再剪,展开即得到图案).

下面四个图案,不能用上述方法剪出的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 小题易丢分 题型:填空题
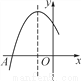
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出以下结论:①abc<0;②b2-4ac>0;③4b+c<0;④若B(-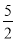 ,y1),C(-
,y1),C(-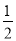 ,y2)为函数图象上的两点,则y1>y2;⑤当-3≤x≤1时,y≥0,其中正确的结论是______.(填序号)
,y2)为函数图象上的两点,则y1>y2;⑤当-3≤x≤1时,y≥0,其中正确的结论是______.(填序号)
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 小题易丢分 题型:单选题
因为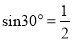 ,
, 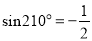 ,所以
,所以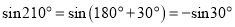 ;因为
;因为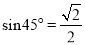 ,
, 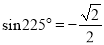 ,所以
,所以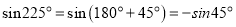 ,由此猜想,推理知:一般地当
,由此猜想,推理知:一般地当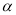 为锐角时有
为锐角时有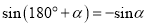 ,由此可知:
,由此可知: 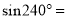 ( ).
( ).
A. 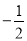 B.
B. 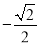 C.
C. 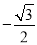 D.
D. 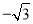
查看答案和解析>>
科目:初中数学 来源:甘肃省武威市2017-2018学年八年级(上)期中数学试卷 题型:解答题
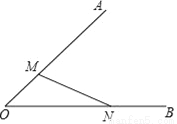
在图中求作一点P,使点P到∠AOB两边的距离相等,并且使OP等于MN,不写作法,保留作图痕迹.(要求:用尺规作图)
查看答案和解析>>
科目:初中数学 来源:2017年广东省韶关市南雄市中考数学模拟试卷 题型:解答题
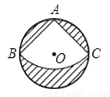
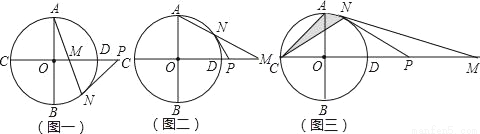
如图,⊙O的半径为1,直线CD经过圆心O,交⊙O于C、D两点,直径AB⊥CD,点M是直线CD上异于点C、O、D的一个动点,AM所在的直线交于⊙O于点N,点P是直线CD上另一点,且PM=PN.
(1)当点M在⊙O内部,如图一,试判断PN与⊙O的关系,并写出证明过程;
(2)当点M在⊙O外部,如图二,其它条件不变时,(1)的结论是否还成立?请说明理由;
(3)当点M在⊙O外部,如图三,∠AMO=15°,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com