
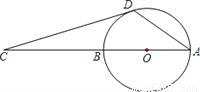
如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=20°,则∠CDA=_____.
科目:初中数学 来源:2017年天津二十一中中考数学冲刺试卷(一) 题型:单选题
如图,等腰三角形ABC中,AB=AC,BD平分∠ABC,∠A=36°,则∠1的度数为( )
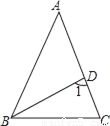
A. 36° B. 60° C. 72° D. 108°
C 【解析】根据∠A=36°,AB=AC求出∠ABC的度数,根据角平分线的定义求出∠ABD的度数,根据三角形的外角的性质计算得到答案. 【解析】 ∵∠A=36°,AB=AC,∴∠ABC=∠C=72°,∵BD平分∠ABC,∴∠ABD=36°,∴∠1=∠A+∠ABD=72°, 故选C.查看答案和解析>>
科目:初中数学 来源:湖南省新化县2016-2017学年度第二学期期中检测七年级数学试卷 题型:填空题
多项式(x-m)(x-n)的展开结果中x的一次项系数为3,常数项为2,则m2n+mn2的值为 ________.
-6 【解析】【解析】 ∵(x-m)(x-n)=x2-(m+n)x+mn,∴m+n=-3,mn=2,∴m2n+mn2=mn(m+n)=2×(-3)=-6.故答案为:-6.查看答案和解析>>
科目:初中数学 来源:江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型:解答题
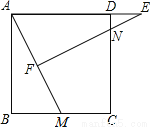
如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM ∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型:填空题
如图,将边长为(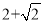 )cm的正方形绕其中心旋转45°,则两个正方形公共部分(图中阴影部分)的面积为___________cm2.
)cm的正方形绕其中心旋转45°,则两个正方形公共部分(图中阴影部分)的面积为___________cm2.
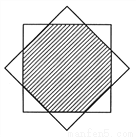
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型:单选题
二次函数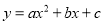 图象上部分点的坐标满足下表,则该函数图象的顶点坐标为
图象上部分点的坐标满足下表,则该函数图象的顶点坐标为
X | … | -3 | -2 | -1 | 0 | 1 | … |
y | … | -3 | -2 | -3 | -6 | -11 | … |
A. (﹣3,﹣3) B. (﹣2,﹣2) C. (﹣1,﹣3) D. (0,﹣6)
B 【解析】∵x=?3和?1时的函数值都是?3相等, ∴二次函数的对称轴为直线x=?2, ∴顶点坐标为(?2,?2). 故选:B.查看答案和解析>>
科目:初中数学 来源:江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型:单选题
抛物线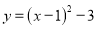 的对称轴是( )
的对称轴是( )
A. y轴 B. 直线x=﹣3 C. 直线x=﹣1 D. 直线x=1
D 【解析】抛物线y=(x-1)2-3是抛物线的顶点式, 根据抛物线的顶点式可知抛物线y=(x-1)2-3的对称轴是直线x=1. 故选C.查看答案和解析>>
科目:初中数学 来源:江苏省泰州市2017年中考数学二模试卷(解析版) 题型:填空题
函数y=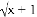 中,自变量x的取值范围是_____.
中,自变量x的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源:湖北省黄冈市2017-2018学年七年级上学期第三次学力检测数学试卷 题型:单选题
下列各对数是互为倒数的是( )
A. 4和-4 B. -3和 C. -2和
C. -2和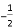 D. 0和0
D. 0和0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com