
计算:
(1)(a+b)(a﹣2b)﹣(a﹣b)2;
(2)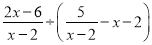 .
.
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源:2017年浙江省台州市中考数学二模试卷 题型:填空题
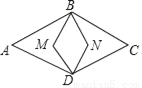
如图,菱形ABCD内两点M、N,满足MB⊥BC,MD⊥DC,NB⊥BA,ND⊥DA,若四边形BMDN的面积是菱形ABCD面积的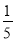 ,则cosA=_____.
,则cosA=_____.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题七年级人教版数学试卷(B卷) 题型:解答题
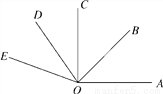
如图所示,OB是∠AOC的平分线,OD是∠COE的平分线.
(1)若∠AOB=50°,∠DOE=35°,求∠BOD的度数;
(2)若∠AOE=160°,∠COD=40°,求∠AOB的度数.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题七年级人教版数学试卷(B卷) 题型:单选题
如图,如果∠AOC=∠BOD,则∠AOB与∠DOC的大小关系是( )
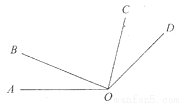
A. ∠AOB>∠DOC B. ∠AOB<∠DOC
C. ∠AOB=∠DOC D. 无法比较
C 【解析】∵∠AOC=∠BOD, ∴∠AOC-∠BOC=∠BOD-∠BOC, ∴∠AOB=∠DOC. 故选C.查看答案和解析>>
科目:初中数学 来源:重庆市2017年中考数学二模试卷 题型:解答题
如图1,在平面直角坐标系中,抛物线y=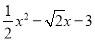 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,抛物线的顶点为点D,过点B作BC的垂线,交对称轴于点E.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,抛物线的顶点为点D,过点B作BC的垂线,交对称轴于点E.
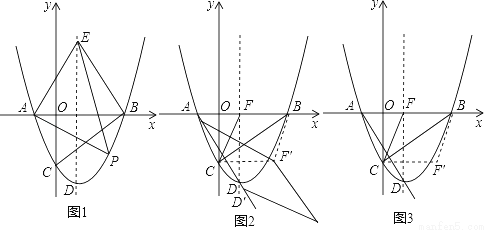
(1)求证:点E与点D关于x轴对称;
(2)点P为第四象限内的抛物线上的一动点,当△PAE的面积最大时,在对称轴上找一点M,在y轴上找一点N,使得OM+MN+NP最小,求此时点M的坐标及OM+MN+NP的最小值;
(3)如图2,平移抛物线,使抛物线的顶点D在射线AD上移动,点D平移后的对应点为D′,点A的对应点A′,设抛物线的对称轴与x轴交于点F,将△FBC沿BC翻折,使点F落在点F′处,在平面内找一点G,若以F′、G、D′、A′为顶点的四边形为菱形,求平移的距离.
(1)证明见解析;(2);(3), , 【解析】试题分析:(1)首先求出A、B、C、D的坐标,再根据△EFB∽△BOC对应边成比例得出方程,推出EF的长度,求出点E的坐标即可解决问题; (2)过点P作PQ∥y轴,交直线AE于点Q.构建 二次函数,利用二次函数的性质求出点P的坐标,作点O关于对称轴的对称点O′,作点P关于Y轴的对称点P′,连接O′P′,分别交对称轴、y轴于点M、N,此时M...查看答案和解析>>
科目:初中数学 来源:重庆市2017年中考数学二模试卷 题型:填空题
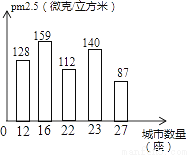
如图是我校某班同学随机抽取的我国100座城市2017年某天当地PM 2.5值的情况的条形统计图,那么本次调查中,PM2.5值的中位数为________微克/立方米.
查看答案和解析>>
科目:初中数学 来源:重庆市2017年中考数学二模试卷 题型:单选题
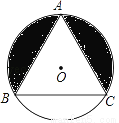
如图,等边△ABC内接于⊙O,已知⊙O的半径为2,则图中的阴影部分面积为( )
A. 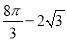 B.
B. 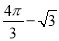 C.
C. 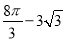 D.
D. 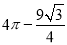
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题七年级浙教版数学试卷(A卷) 题型:填空题
如图,OC是∠AOB的平分线,OD是∠BOC的平分线,则∠COD=______∠AOC, ∠BOD=______∠AOD.
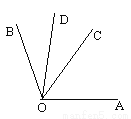
查看答案和解析>>
科目:初中数学 来源:2017年安徽省合肥市高新区梦园学校中考数学模拟试卷 题型:解答题
如图,抛物线y=ax2+bx+c的顶点为M(﹣2,﹣4),与x轴交于A、B两点,且A(﹣6,0),与y轴交于点C.
(1)求抛物线的函数解析式;
(2)求△ABC的面积;
(3)能否在抛物线第三象限的图象上找到一点P,使△APC的面积最大?若能,请求出点P的坐标;若不能,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com