练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知a﹣2b+3=0，则代数式5+2b﹣a的值是（　　）

    A. 2 B. 4 C. 6 D. 8

    D 【解析】试题分析：根据题意，可先由a-2b+3=0变形可得2b-a=3，然后整体代入即可得：5+2b-a=5+3=8. 故选：D.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年海南省中考数学模拟试卷 题型：解答题

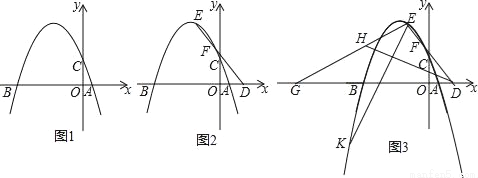
    如图1，已知抛物线y=﹣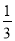x2﹣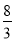x+c与x轴相交于A、B两点（B点在A点的左侧），与y轴相交于C点，且AB=10．

    （1）求这条抛物线的解析式；

    （2）如图2，D点在x轴上，且在A点的右侧，E点为抛物线上第二象限内的点，连接ED交抛物线于第二象限内的另外一点F，点E到y轴的距离与点F到y轴的距离之比为3：1，已知tan∠BDE=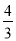，求点E的坐标；

    （3）如图3，在（2）的条件下，点G由B出发，沿x轴负方向运动，连接EG，点H在线段EG上，连接DH，∠EDH=∠EGB，过点E作EK⊥DH，与抛物线相应点E，若EK=EG，求点K的坐标．

    （1）y=﹣x2﹣x+3；（2）E（﹣3，8）；（3）K(-11，-8). 【解析】试题分析：（1）先根据函数关系式求出对称轴，由AB=10，，求出点的坐标，代入函数关系式求出的值，即可解答； （2）作EM⊥x轴，垂足为点M，FN⊥x轴，垂足为点N，FT⊥EM，垂足为点T.得到四边形FTMN为矩形，由, ,得到∠BDE=∠EFT，所以设设 得到 再由解得 代入函数关系式即可解答； （3）...

    查看答案和解析>>

    科目：初中数学 来源：福建省2017-2018学年七年级上学期期中考试数学试卷 题型：单选题

    合并同类项﹣2xy+8xy=（﹣2+8）xy=6xy时，依据的运算律是（　　）

    A. 加法交换律 B. 乘法交换律 C. 乘法结合律 D. 乘法分配律

    D 【解析】∵合并同类项是逆用乘法的分配律， ∴合并同类项的依据是乘法的分配律. 故选D.

    查看答案和解析>>

    科目：初中数学 来源：山东省寿光市2017-2018学年七年级上期末模拟数学试卷 题型：填空题

    点A在数轴上所表示的数为﹣1，若AB=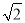，则点B在数轴上所表示的数为________．

    【解析】B点在A点的右边时，B点的坐标为﹣1+； B点在A点的左边时，B点的坐标为﹣1﹣； 故答案为：﹣1+，或﹣1﹣．

    查看答案和解析>>

    科目：初中数学 来源：山东省寿光市2017-2018学年七年级上期末模拟数学试卷 题型：单选题

    已知两数相乘大于0，两数相加小于0，则这两数的符号为（　　）

    A. 同正 B. 同负 C. 一正一负 D. 无法确定

    B 【解析】【解析】 ∵两数相乘大于0，则两数同号， 又∵两数相加小于0， 则这两数为同负． 故选B

    查看答案和解析>>

    科目：初中数学 来源：2017年天津二十一中中考数学冲刺试卷（2） 题型：解答题

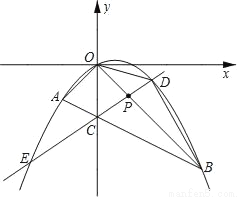
    如图，在平面直角坐标系中，点A的坐标为（m，m），点B的坐标为（n，﹣n），抛物线经过A、O、B三点，连接OA、OB、AB，线段AB交y轴于点C．已知实数m、n（m＜n）分别是方程x2﹣2x﹣3=0的两根．

    （1）求抛物线的解析式；

    （2）若点P为线段OB上的一个动点（不与点O、B重合），直线PC与抛物线交于D、E两点（点D在y轴右侧），连接OD、BD．

    ①当△OPC为等腰三角形时，求点P的坐标；

    ②求△BOD 面积的最大值，并写出此时点D的坐标．

    （1）y=x2+x；（2）①P点坐标为P1（，-）或P2（，﹣）或P3（，﹣），②D（，﹣）． 【解析】试题分析：（1）首先解方程得出A，B两点的坐标，进而利用待定系数法求出二次函数解析式即可； （2）①首先求出AB的直线解析式，以及BO解析式，再利用等腰三角形的性质得出当OC=OP时，当OP=PC时，点P在线段OC的中垂线上，当OC=PC时分别求出x的值即可； ②利用S△BOD=S△O...

    查看答案和解析>>

    科目：初中数学 来源：2017年天津二十一中中考数学冲刺试卷（2） 题型：填空题

    某商店进了一批货，每件3元，出售时每件加价0.5元，如售出x件应收入货款y元，那么y(元)与x(件)的函数表达式是_________________．

    y=3.5x 【解析】根据总价=单价×数量，单价为（3+0.5）元，可得：y=（3+0.5）x=3.5x．故y与x的函数关系式是：y=3.5x． 故答案为：y=3.5x．

    查看答案和解析>>

    科目：初中数学 来源：2017年吉林省中考数学一诊试卷 题型：解答题

    已知关于x的一元二次方程x2﹣2（m+1）x+m2+2=0

    （1）若方程有实数根，求实数m的取值范围；

    （2）若方程两实数根分别为x1、x2，且满足x12+x22=10，求实数m的值．

    （1）m≥（2）实数m的值为1． 【解析】试题分析：（1）根据方程的系数结合根的判别式即可得出关于m的一元一次不等式，解之即可得出结论； （2）根据根与系数的关系即可得出x1+x2=2（m+1）、x1•x2=m2+2，结合x12+x22=10即可得出关于m的一元二次方程，解之即可得出m的值，再结合（1）的结论即可得出结论． 试题解析：（1）∵方程x2﹣2（m+1）x+m2+2=0...

    查看答案和解析>>

    科目：初中数学 来源：2017年贵州省中考数学二模试卷 题型：单选题

    下列运算正确的是（ ）

    A．a2+a3=a5 B．a2•a3=a6 C．（a2b3）3=a5b6 D．（a2）3=a6

    D． 【解析】 试题解析：A、a2与a3不是同类项不能合并，故本选项错误； B、应为a2•a3=a5，故本选项错误； C、应为（a2b3）3=a6b9，故本选项错误； D、（a2）3=a6，正确； 故选D．

    查看答案和解析>>

    同步练习册答案