
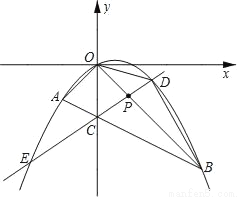
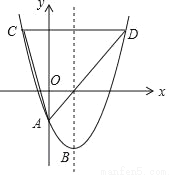
��ͼ����ƽ��ֱ������ϵ�У���A������Ϊ��m��m������B������Ϊ��n����n���������߾���A��O��B���㣬����OA��OB��AB���߶�AB��y���ڵ�C����֪ʵ��m��n��m��n���ֱ��Ƿ���x2��2x��3=0��������
��1���������ߵĽ���ʽ��
��2������PΪ�߶�OB�ϵ�һ�����㣨�����O��B�غϣ���ֱ��PC�������߽���D��E���㣨��D��y���Ҳࣩ������OD��BD��
�ٵ���OPCΪ����������ʱ�����P�����ꣻ
�����BOD ��������ֵ����д����ʱ��D�����꣮

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017�꺣��ʡ�п���ѧģ���Ծ� ���ͣ������
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ�����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ���ѡ��
��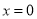 �ǹ���
�ǹ���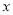 �ķ���
�ķ���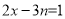 �Ľ�.��
�Ľ�.��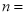 �� ��.
�� ��.
A. 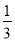 B. 3 C.
B. 3 C. 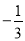 D.
D. 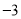
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ�ٹ���2017-2018ѧ�����꼶����ĩģ����ѧ�Ծ� ���ͣ������
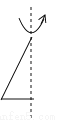
��ͼ��ʾ��ͼ����������תһ�ܵõ��ļ������������________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ�ٹ���2017-2018ѧ�����꼶����ĩģ����ѧ�Ծ� ���ͣ���ѡ��
��֪a��2b+3=0�������ʽ5+2b��a��ֵ�ǣ�������
A. 2 B. 4 C. 6 D. 8
D ������������������������⣬������a-2b+3=0���οɵ�2b-a=3��Ȼ��������뼴�ɵã�5+2b-a=5+3=8. ��ѡ��D.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017������ʮһ���п���ѧ����Ծ���2�� ���ͣ������
һ��Բ�����Ź��Ĺ���Ϊ1�ף����Ϊ4�ף���ô����Ź��İ뾶Ϊ________��.
2.5. ����������뾶Ϊrm�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017������ʮһ���п���ѧ����Ծ���2�� ���ͣ���ѡ��
��ͼ����O�İ뾶Ϊ5����AB�ij�Ϊ8��M����AB�ϵĶ��㣬���߶�OM������СֵΪ��������
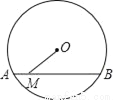
A. 2 B. 3 C. 4 D. 5
B ��������������������ݴ��߶���̿�֪����ʱ���߶�OM��ֵ��С ��ʱ������OA���ɴ���������֪�� ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�꼪��ʡ�п���ѧһ���Ծ� ���ͣ������
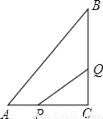
��ͼ����ABC�У���C=90�㣬AC=6��BC=8������P��A���������1cm/s���ٶȣ���A��C��B��B���˶���ͬʱ������Q��C���������2cm/s���ٶȣ���C��B��A��A���˶���������һ���˶����յ�ʱ������ͬʱֹͣ�˶������˶�ʱ��Ϊt�룬��t=_____��ʱ����PCQ���������8cm2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�꼪��ʡ�������п���ѧģ���Ծ���7�� ���ͣ������
��ͼ����ƽ��ֱ������ϵ�У�������y=a��x��2��2��4��y�ύ�ڵ�A������ΪB����A������Ϊ��0����2������C���������ϣ������A��B�غϣ�������C��y��Ĵ��߽��������ڵ�D������AC��AD��CD�����C�ĺ�����Ϊm��
��1������������������Ӧ�ĺ�������ʽ��
��2���ú�m�Ĵ���ʽ��ʾ�߶�CD�ij���
��3����E�������߶Գ�����һ�㣬�ҵ�E��������ȵ�C��������С1������BD��DE�����ACD�����ΪS1����BDE�����ΪS2����S1•S2��0����S2=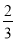 S1ʱm��ֵ��
S1ʱm��ֵ��
��4����������y=a��x��2��2��4��x=2ƽ�ƣ��õ�������y=a��x��2��2+k������C��y��ƽ������������y=a��x��2��2+k���ڵ�F����CD��y�ύ�ڵ�G����CD=6��ֱ��д��ʹAC=FG�ĵ�F�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com