
如图,在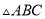 中,
中, 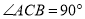 ,点D, E分别在
,点D, E分别在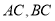 上,且
上,且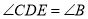 ,将
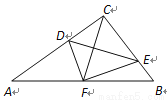
,将 沿DE折叠,点C恰好落在AB边上的点F处,如果
沿DE折叠,点C恰好落在AB边上的点F处,如果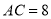 ,
, 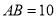 ,那么CD的长为__________.
,那么CD的长为__________.
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源:2017-2018学年度第一学期海南省九年级数学科期末检测模拟试卷 题型:填空题
在正方形网格中,∠AOB的位置如图所示,则tan∠AOB的值为______.

查看答案和解析>>
科目:初中数学 来源:山东省淄博市2018届九年级上学期期中考试数学试卷 题型:解答题
为了普及环保知识,增强环保意识,某中学组织了环保知识竞赛,初中三个年级根据初赛成绩分别选出了10名同学参加决赛,这些选手的决赛成绩(满分为100分)如下表所示:
年级 | 决赛成绩(单位:分) | |||||||||
七年级 | 80 | 86 | 88 | 80 | 88 | 99 | 80 | 74 | 91 | 89 |
八年级 | 85 | 85 | 87 | 97 | 85 | 76 | 88 | 77 | 87 | 88 |
九年级 | 82 | 80 | 78 | 78 | 81 | 96 | 97 | 88 | 89 | 86 |
(1)请你填写下表:
年级 | 平均数 | 众数 | 中位数 |
七年级 | 85.5 | 87 | |
八年级 | 85.5 | 85 | |
九年级 | 84 |
(2)请从以下两个不同的角度对三个年级的决赛成绩进行分析:
①从平均数和众数相结合看(分析哪个年级成绩好些);
②从平均数和中位数相结合看(分析哪个年级成绩好些)
③如果在每个年级分别选出3人参加决赛,你认为哪个年级的实力更强一些?并说明理由.
(1)填表见解析(2)①八年级②七年级③九年级 【解析】(1)平均数的计算方法是求出所有数据的和,然后除以数据的总个数.对于中位数, 因图中是按从小到大的顺序排列的,所以只要找出最中间的一个数(或最中间的两个数)即 可,本题是最中间两个数的平均数.对于众数是出现次数最多的数据; (2)可由(1)得出的表格,将三个年级的平均数,众数和中位数进行比较即可得出正确的 结论;...查看答案和解析>>
科目:初中数学 来源:山东省淄博市2018届九年级上学期期中考试数学试卷 题型:单选题
若把分式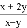 中的
中的
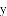
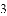
A. 扩大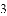
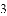
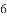
查看答案和解析>>
科目:初中数学 来源:上海市崇明区2018届九年级上学期期末调研测试数学试卷 题型:解答题
如图,点E是正方形ABCD的边BC延长线上一点,联结DE,过顶点B作 ,垂足为F,BF交边DC于点G.
,垂足为F,BF交边DC于点G.
(1)求证:  ;
;
(2)连接CF,求证:  .
.

查看答案和解析>>
科目:初中数学 来源:上海市崇明区2018届九年级上学期期末调研测试数学试卷 题型:填空题
在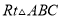 中,
中, 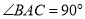 ,
, 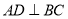 ,垂足为点D,如果
,垂足为点D,如果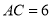 ,
, 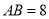 ,那么AD的长度为________.
,那么AD的长度为________.
查看答案和解析>>
科目:初中数学 来源:上海市崇明区2018届九年级上学期期末调研测试数学试卷 题型:单选题
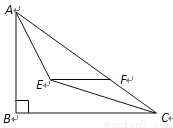
如图,在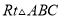 中,
中, 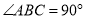 ,
, 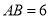 ,
, 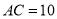 ,
, 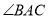 和
和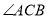 的平分线相交于点E,过点E作
的平分线相交于点E,过点E作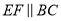 交
交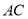 于点F,那么EF的长为( )
于点F,那么EF的长为( )
A. 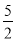 B.
B. 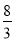 C.
C. 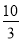 D.
D. 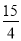
查看答案和解析>>
科目:初中数学 来源:江苏省南京市建邺区2016-2017学年度第一学期期末调研测试九年级数学试卷 题型:填空题
如图,AB=5,P是线段AB上的动点,分别以AP、BP为边,在线段AB的同侧作正方形APCD和正方形BPEF,连接CF,则CF的最小值是____.
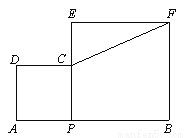
查看答案和解析>>
科目:初中数学 来源:广东省江门市江海区五校2018届九年级上学期期末联考数学试卷 题型:解答题
如图,一次函数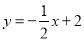 分别交y轴、x 轴于A、B两点,抛物线
分别交y轴、x 轴于A、B两点,抛物线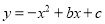 过A、B两点.
过A、B两点.
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于点M,交这个抛物线于点N.求当t 取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
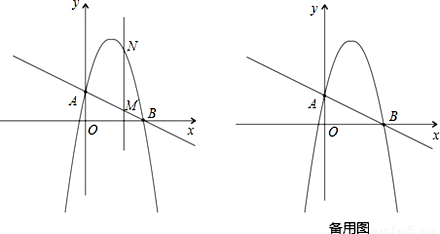
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com