
已知在 中,AB= AC=5,BC=6,则tanB的值为_____.
中,AB= AC=5,BC=6,则tanB的值为_____.
科目:初中数学 来源:2017-2018学年八年级数学下册(人教版):期末检测题(二) 题型:单选题
一次函数y=kx+b(k,b是常数,k≠0)的图象如图所示,则不等式kx+b>0的解集是( )
A. x>-2 B. x>0 C. x<-2 D. x<0
A 【解析】∵不等式kx+b>0的解集是一次函数图象位于x轴上方部分图象所对应的自变量的取值范围, ∴由图可得不等式kx+b>0的解集为:x>-2. 故选A.查看答案和解析>>
科目:初中数学 来源:辽宁省抚顺县2018届九年级上学期期末教学质量检测数学试卷 题型:填空题
如图,△ABC内接于⊙O,AB=BC,∠ABC=120°,AD为⊙O直径,AD=8,那么AB的长为_____.
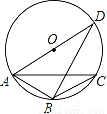
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2017-2018学年九年级上学期期末考试数学试卷 题型:解答题
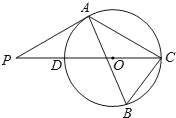
如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若AB=4+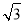 ,BC=2
,BC=2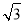 ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2017-2018学年九年级上学期期末考试数学试卷 题型:填空题
关于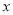 的方程
的方程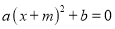 的解是
的解是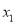 =
=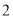 ,
, 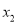 =
=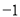 (
(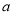 、
、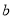 、
、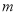 为常数,
为常数, 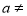 0),则方程
0),则方程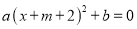 的解是_____.
的解是_____.
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2017-2018学年九年级上学期期末考试数学试卷 题型:单选题
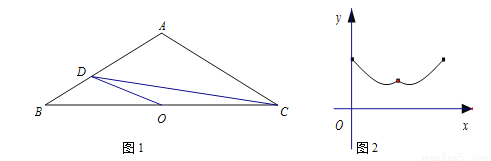
如图1,在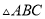 中,
中, 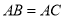 ,
, 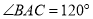 .点O是BC的中点,点D沿B→A→C方向从B运动到C.设点D经过的路径长为
.点O是BC的中点,点D沿B→A→C方向从B运动到C.设点D经过的路径长为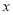 ,图1中某条线段的长为y,若表示y与x的函数关系的大致图象如图2所示,则这条线段可能是图1中的( )
,图1中某条线段的长为y,若表示y与x的函数关系的大致图象如图2所示,则这条线段可能是图1中的( )
A. 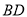 B.
B.  C.
C.  D.
D. 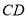
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2017-2018学年九年级上学期期末考试数学试卷 题型:单选题
关于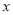 的一元二次方程
的一元二次方程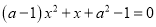 的一个根是0,则
的一个根是0,则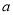 值为( )
值为( )
A. 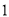 B.
B. 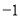 C.
C. 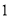 或
或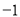 D.
D. 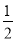
查看答案和解析>>
科目:初中数学 来源:2017-2018学年福建省龙岩市上杭县城区片三校七年级(上)联考数学试卷 题型:单选题
已知某商店有两个进价不同的计算器都卖了80元,其中一个盈利60%,另一个亏损20%,在这次买卖中,这家商店( )
A. 不盈不亏 B. 盈利10元 C. 亏损10元 D. 盈利50元
B 【解析】试题解析:设盈利的进价是x元, 80-x=60%x x=50 设亏本的进价是y元 y-80=20%y y=100 80+80-100-50=10元. 故赚了10元. 故选B.查看答案和解析>>
科目:初中数学 来源:吉林省四平市 2017-2018学年第一学期八年级数学期末综合检测卷 题型:解答题
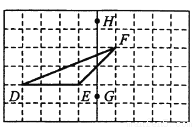
如图,在正方形网格上有一个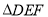 .
.
(1)画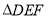 关于直线
关于直线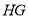 的轴对称图形.
的轴对称图形.
(2)画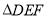 的
的 边上的高.
边上的高.
(3)若网格上的最小正方形边长为1,求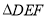 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com