
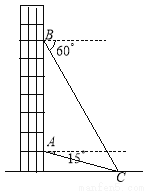
从一幢建筑大楼的两个观察点A,B观察地面的花坛(点C),测得俯角分别为15°和60°,如图,直线AB 与地面垂直,AB=50米,试求出点B到点C的距离.(结果保留根号)
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:山东省2017-2018学年七年级上期末复习检测数学试卷 题型:填空题
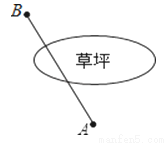
如图,从教室门B到图书馆A,总有一些同学不文明,为了走捷径,不走人行道而横穿草坪,其中包含的数学几何知识为:________
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(三) 题型:解答题
如图1,正方形ABCD的一边AB在直尺一边所在直线MN上,点O是对角线AC、BD的交点,过点O作OE⊥MN于点E.
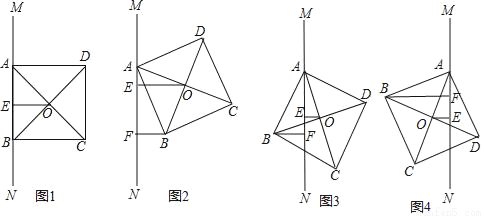
(1)如图1,线段AB与OE之间的数量关系为 .(请直接填结论)
(2)保证点A始终在直线MN上,正方形ABCD绕点A旋转θ(0<θ<90°),过点 B作BF⊥MN于点F.
①如图2,当点O、B两点均在直线MN右侧时,试猜想线段AF、BF与OE之间存在怎样的数量关系?请说明理由.
②如图3,当点O、B两点分别在直线MN两侧时,此时①中结论是否依然成立呢?若成立,请直接写出结论;若不成立,请写出变化后的结论并证明.
③当正方形ABCD绕点A旋转到如图4的位置时,线段AF、BF与OE之间的数量关系为 .(请直接填结论)
(1)AB=2OE;(2)①AF+BF=2OE,证明见解析;②AF﹣BF=2OE 证明见解析;③BF﹣AF=2OE, 【解析】试题分析:(1)利用直角三角形斜边的中线等于斜边的一半即可得出结论; (2)①过点B作BH⊥OE于H,可得四边形BHEF是矩形,根据矩形的对边相等可得EF=BH,BF=HE,根据正方形的对角线相等且互相垂直平分可得OA=OB,∠AOB=90°,再根据同角的余角相...查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(三) 题型:单选题
在△ABC中,∠A=120°,AB=4,AC=2,则sinB的值是( )
A. 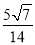 B.
B. 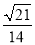 C.
C. 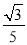 D.
D. 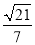
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(三) 题型:单选题
﹣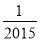 的倒数是( )
的倒数是( )
A. 2015 B. ﹣2015 C. 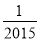 D. ﹣
D. ﹣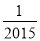
查看答案和解析>>
科目:初中数学 来源:2017年湖南省郴州市资兴市兴华实验学校中考数学模拟试卷 题型:解答题
计算: 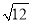 +|
+|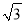 ﹣3|﹣2sin60°﹣(
﹣3|﹣2sin60°﹣(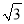 )2+20160.
)2+20160.
查看答案和解析>>
科目:初中数学 来源:2017年湖南省郴州市资兴市兴华实验学校中考数学模拟试卷 题型:填空题
分解因式2x2﹣4x+2的最终结果是_____.
2(x﹣1)2 【解析】试题分析:先提取公因式2,再根据完全平方公式进行二次分解. 试题解析:2x2-4x+2, =2(x2-2x+1), =2(x-1)2.查看答案和解析>>
科目:初中数学 来源:辽宁省抚顺县2017-2018学年八年级上学期期末教学质量检测数学试卷 题型:填空题
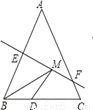
如图,等腰三角形ABC的底边BC长为4,面积是12,腰AB的垂直平分线EF分别交AB,AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为_____________
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市邗江区2018届九年级(上)期中数学试卷 题型:单选题
如图,圆锥的底面半径OB=6cm,高OC=8cm.则这个圆锥的侧面积是( )
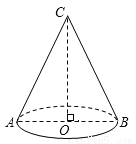
A. 30cm2 B. 30πcm2 C. 60πcm2 D. 120cm2
C 【解析】试题分析:先利用勾股定理计算出圆锥的母线长=,然后利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形面积公式计算这个圆锥漏斗的侧面积=•2π•6•10=60π(cm2). 故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com