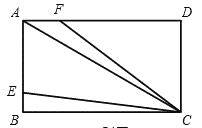
如图，AC是矩形ABCD的对角线，AB=2，BC=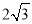
，点E、F分别是线段AB，AD上的点，连接CE，CF，当∠BCE=∠ACF，且CE=CF时，AE+AF=______．
科目：初中数学 来源：2018年河北省邯郸市初三中考一模数学试卷 题型：单选题
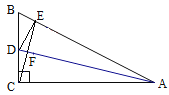
如图，Rt△ABC中，∠ACB＝90°，∠BAC＝30°，∠BAC的平分线交BC于点D，过点D作DE⊥AB，垂足为E，连接CE交AD于点F，则以下结论：①AB＝2CE； ②AC＝4CD；③CE⊥AD； ④△DBE与△ABC的面积比是：1：（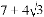
）其中正确结论是（ ）
A. ①② B. ②③ C. ③④ D. ①④
查看答案和解析>>
科目：初中数学 来源：2017-2018学年河南省九年级（上）期中数学试卷 题型：解答题
如图，已知反比例函数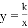
与一次函数y=x+b的图象在第一象限相交于点A（1，﹣k+4）．
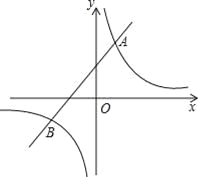
（1）试确定这两个函数的表达式；
（2）求出这两个函数图象的另一个交点B的坐标，并根据图象写出使反比例函数的值大于一次函数的值的x的取值范围．
查看答案和解析>>
科目：初中数学 来源：2017-2018学年河南省九年级（上）期中数学试卷 题型：单选题
如图，在△ABC中E、F分别是AB、AC上的点，EF∥BC，且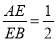
，若△AEF的面积为2，则四边形EBCF的面积为 （ ）
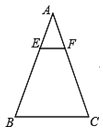
A. 4 B. 6 C. 16 D. 18
查看答案和解析>>
科目：初中数学 来源：2018年浙江省宁波市鄞州区中考数学模拟试卷（4月份） 题型：解答题
（2017四川省攀枝花市，第20题，8分）攀枝花芒果由于品质高、口感好而闻名全国，通过优质快捷的网络销售渠道，小明的妈妈先购买了2箱A品种芒果和3箱B品种芒果，共花费450元；后又购买了l箱A品种芒果和2箱B品种芒果，共花费275元（每次两种芒果的售价都不变）．
（1）问A品种芒果和B品种芒果的售价分别是每箱多少元？
（2）现要购买两种芒果共18箱，要求B品种芒果的数量不少于A品种芒果数量的2倍，但不超过A品种芒果数量的4倍，请你设计购买方案，并写出所需费用最低的购买方案．
查看答案和解析>>
科目：初中数学 来源：2018年浙江省宁波市鄞州区中考数学模拟试卷（4月份） 题型：单选题
如图，直线a||b，直线l与a，b分别相交于A，B两点，AC⊥AB交b于点C，∠1=40°，则∠2的度数是（ ）
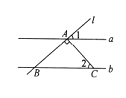
A. 40° B. 45° C. 50° D. 60°
查看答案和解析>>
科目：初中数学 来源：江苏省无锡新吴区2016-2017学年第二学期4月八年级数学期中试卷 题型：填空题
在矩形ABCD中，对角线AC、BD交于点O，若∠AOB=100°，则∠OAB=___________度．
查看答案和解析>>
科目：初中数学 来源：2018年天津市红桥区中考数学模拟试卷（解析） 题型：解答题
在平面直角坐标系中，O为原点，点A（1，0），点B（0，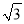 
），把△ABO绕点O顺时针旋转，得A′B′O，记旋转角为α．
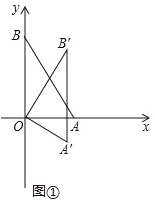
（Ⅰ）如图①，当α=30°时，求点B′的坐标；
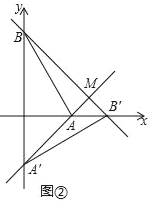
（Ⅱ）设直线AA′与直线BB′相交于点M．
如图②，当α=90°时，求点M的坐标；
②点C（﹣1，0），求线段CM长度的最小值．（直接写出结果即可）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
