
如图,在平面直角坐标系中,矩形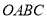 的顶点
的顶点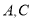 分别在
分别在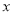 轴,
轴,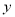 轴的正半轴上,且
轴的正半轴上,且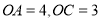 .若抛物线经过
.若抛物线经过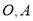 两点,且顶点在
两点,且顶点在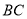 边上,对称轴交
边上,对称轴交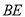 于点
于点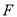 ,点
,点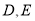 的坐标分别为
的坐标分别为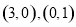 .
.
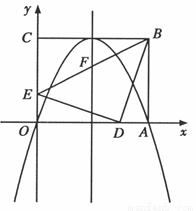
(1)求抛物线的解析式;
(2)猜想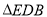 的形状并加以证明;
的形状并加以证明;
(3)点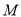 在对称轴右侧的抛物线上,点
在对称轴右侧的抛物线上,点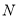 在
在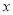 轴上,请问是否存在以点
轴上,请问是否存在以点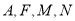 为顶点的四边形是平行四边形?若存在,请求出所有符合条件的点
为顶点的四边形是平行四边形?若存在,请求出所有符合条件的点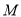 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2017年初中毕业升学考试(吉林卷)数学(解析版) 题型:选择题
如图,在△ABC中,以点B为圆心,以BA长为半径画弧交边BC于点D,连接AD.若∠B=40°,∠C=36°,则∠DAC的度数是( )
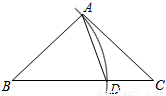
A.70° B.44° C.34° D.24°
查看答案和解析>>
科目:初中数学 来源:2017年初中毕业升学考试(山东滨州卷)数学(解析版) 题型:选择题
在平面直角坐标系内,直线AB垂直于x轴于点C(点C在原点的右侧),并分别与直线y=x和双曲线y=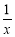 相交于点A、B,且AC+BC=4,则△OAB的面积为
相交于点A、B,且AC+BC=4,则△OAB的面积为
A.2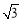 +3或2
+3或2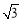 -3 B.
-3 B.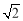 +1或
+1或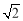 -1
-1
C.2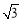 -3 D.
-3 D.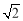 -1
-1
查看答案和解析>>
科目:初中数学 来源:2017年初中毕业升学考试(青海西宁卷)数学(解析版) 题型:解答题
如图,四边形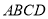 中,
中,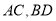 相交于点
相交于点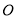 ,
,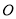 是
是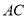 的中点,
的中点,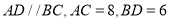 .
.
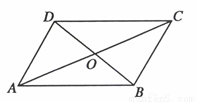
(1)求证:四边形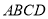 是平行四边形;
是平行四边形;
(2)若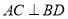 ,求
,求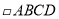 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源:2017年初中毕业升学考试(宁夏卷)数学(解析版) 题型:解答题
为确保广大居民家庭基本用水需求的同时鼓励家庭节约用水,对居民家庭每户每月用水量采用分档递增收费的方式,每户每月用水量不超过基本用水量的部分享受基本价格,超出基本用水量的部分实行超价收费.为对基本用水量进行决策,随机抽查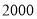 户居民家庭每户每月用水量的数据,整理绘制出下面的统计表:
户居民家庭每户每月用水量的数据,整理绘制出下面的统计表:

(1)为确保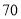 %的居民家庭每户每月的基本用水量需求,那么每户每月的基本用水量最低应确定为多少立方米?
%的居民家庭每户每月的基本用水量需求,那么每户每月的基本用水量最低应确定为多少立方米?
(2)若将(1)中确定的基本用水量及其以内的部分按每立方米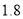 元交费,超过基本用水量的部分按每立方米
元交费,超过基本用水量的部分按每立方米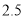 元交费.设
元交费.设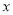 表示每户每月用水量(单位:
表示每户每月用水量(单位: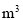 ),
),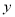 表示每户每月应交水费(单位:元),求
表示每户每月应交水费(单位:元),求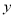 与
与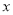 的函数关系式;
的函数关系式;
(3)某户家庭每月交水费是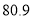 元,请按以上收费方式计算该家庭当月用水量是多少立方米?
元,请按以上收费方式计算该家庭当月用水量是多少立方米?
查看答案和解析>>
科目:初中数学 来源:2017年初中毕业升学考试(内蒙古呼和浩特卷)数学(解析版) 题型:选择题
如图,四边形 是边长为1的正方形,
是边长为1的正方形, ,
, 为
为 所在直线上的两点,若
所在直线上的两点,若 ,
, ,则以下结论正确的是( )
,则以下结论正确的是( )

A. B.
B. C.
C. D.四边形
D.四边形 的面积为
的面积为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com