
已知实数a,b,c满足a>b,c是任意实数,则下列不等式中总是成立的是( )
A. a+c<b+c B. a-c>b-c C. ac<bc D. ac>bc
B 【解析】试题分析:当c=0时,已知A:a>b,则a+c>b+c。不符;C和D:ac=bc=0,不符;故选B科目:初中数学 来源:四川省遂宁市2017-2018学年八年级上学期教学水平监测数学试卷 题型:填空题
在△ABC中,AB=15,AC=13,高AD=12,则BC的长是__________.
14或4 【解析】试题分析:本题应分两种情况进行讨论: (1)当△ABC为锐角三角形时,在Rt△ABD和Rt△ACD中,运用勾股定理可将BD和CD的长求出,两者相加即为BC的长,从而可将△ABC的周长求出; (2)当△ABC为钝角三角形时,在Rt△ABD和Rt△ACD中,运用勾股定理可将BD和CD的长求出,两者相减即为BC的长,从而可将△ABC的周长求出. 【解析】 此题...查看答案和解析>>
科目:初中数学 来源:2016-2017学年内蒙古呼伦贝尔市七年级(下)期中数学试卷 题型:单选题
下列方程组中,是二元一次方程组的是( )
A. 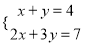 B.
B. 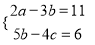 C.
C. 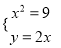 D.
D. 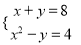
查看答案和解析>>
科目:初中数学 来源:2017-2018学年北师大版八年级数学下册 期中测评 题型:填空题
如图所示,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为点D,若ED=5,则CE的长为_______.

查看答案和解析>>
科目:初中数学 来源:2017-2018学年北师大版八年级数学下册 期中测评 题型:单选题
如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有( )
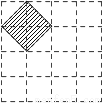
A. 2种B、3种C、4种D、5种
C 【解析】试题分析:利用轴对称图形的性质以及中心对称图形的性质分析得出符合题意的图形即可. 【解析】 如图所示:组成的图形是轴对称图形,又是中心对称图形, 则这个格点正方形的作法共有4种. 故选:C.查看答案和解析>>
科目:初中数学 来源:四川省遂宁市2018届九年级上学期教学水平监测数学试卷 题型:解答题
在北京2008年第29届奥运会前夕,某超市在销售中发现:奥运会吉祥物— “福娃”平均每天可售出20套,每件盈利40元。为了迎接奥运会,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存。经市场调查发现:如果每套降价4元,那么平均每天就可多售出8套。要想平均每天在销售吉祥物上盈利1200元,那么每套应降价多少?
每套应降价20元. 【解析】试题分析:设每套降价x元,那么就多卖出2x套,根据扩大销售量,增加盈利,尽快减少库存,每天在销售吉祥物上盈利1200元,可列方程求解. 试题解析:设每套降价x元, 由题意得:(40-x)(20+2x)=1200 即2x2-60x+400=0, ∴x2-30x+200=0, ∴(x-10)(x-20)=0, 解之得:x=10或x=...查看答案和解析>>
科目:初中数学 来源:四川省遂宁市2018届九年级上学期教学水平监测数学试卷 题型:填空题
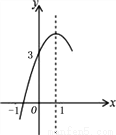
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与 轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
① 4ac<b2;② 方程ax2+bx+c=0的两个根是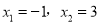 ;③ 3a+c>0;④ 当y>0时,x的取值范围是-1≤x<3;⑤ 当x<0时,y随x增大而增大;
;③ 3a+c>0;④ 当y>0时,x的取值范围是-1≤x<3;⑤ 当x<0时,y随x增大而增大;
其中结论正确有__________.
查看答案和解析>>
科目:初中数学 来源:四川省遂宁市2018届九年级上学期教学水平监测数学试卷 题型:单选题
若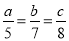 ,且
,且 ,则
,则 的值为:
的值为:
A. 14 B. 42 C. 7 D. 
查看答案和解析>>
科目:初中数学 来源:2018春季学北师大版九年级数学下册期中测评试卷 题型:填空题
若点P(1,a),Q(-1,b)都在抛物线y=-x2+1上,则线段PQ的长为_____.
2 【解析】试题解析:将点P(1,a),Q(-1,b)的坐标分别代入y=-x2+1,得a=0,b=0. 故线段PQ的长为2. 故答案为:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com