练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下列方程是一元二次方程的是（　　）

    A. 3x2+=0 B. 2x﹣3y+1=0 C. （x﹣3）（x﹣2）=x2 D. （3x﹣1）（3x+1）=3

    D 【解析】A.3x2+=0是分式方程，故此选项错误； B.2x?3y+1=0为二元一次方程，故此选项错误； C.(x?3)(x?2)=x2是一元一次方程，故此选项错误； D.(3x?1)(3x+1)=3是一元二次方程，故此选项正确。 故选D.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版数学七年级下册第一章整式乘法1.2幂的乘方与积的乘方课时练习 题型：单选题

    （-5b）3等于（ ）

    A. －125b3 B. 125b10 C. 15b9 D. 125b3

    A 【解析】试题解析： ，故A项正确. 故选A.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年九年级数学北师大版上册 第2章 一元二次方程 单元测试卷 题型：解答题

    用适当的方法解下列方程：

    (1)(6x－1)2＝25；

    (2)x2－2x＝2x－1；

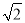    (3)x2－x＝2；

    (4)x(x－7)＝8(7－x)．

    (1) x1＝1，x2＝－；(2) x1＝2＋，x2＝2－；(3)x1＝，x2＝； (4) x1＝7，x2＝－8. 【解析】试题分析：(1)、两边直接开平方得出方程的解；(2)、首先将方程的左边转化为含有x的项，右边保留常数项，然后利用配方法求出方程的解；(3)、首先将方程转化为一般式，然后利用公式法得出方程的解；(4)、首先将方程进行移项，然后利用提取公因式将方程进行因式分解，从而得...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年九年级数学北师大版上册 第2章 一元二次方程 单元测试卷 题型：填空题

    把一元二次方程(x－3)2＝4化为一般形式，其中二次项为_______，一次项系数为_______，常数项为________.

    x2 －6 5 【解析】试题分析：根据完全平方公式去括号可知： ，转化为一般式为： ，则二次项为，一次项系数为-6，常数项为5．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学北师大版上册 第1-4章综合测试卷 题型：解答题

    谷歌人工智能AlphaGo机器人与李世石的围棋挑战赛引起人们的广泛关注，人工智能完胜李世石．某教学网站开设了有关人工智能的课程并策划了A，B两种网上学习的月收费方式：

    收费

    方式

    月使用费(元)

    包时上网

    时间(h)

    超时费(元/min)

    A

    7

    25

    0.6

    B

    10

    50

    0.8

    设小明每月上网学习人工智能课程的时间为x小时，方案A，B的收费金额分别为yA元，yB元．

    (1)当x≥50时，分别求出yA，yB与x之间的函数关系式；

    (2)若小明3月份上该网站学习的时间为60小时，则他选择哪种方式上网学习合算？

    (1) yA＝0.6x－8，yB＝0.8x－30；(2) yA＞yB.故选择B方式上网学习合算． 【解析】试题分析：（1）根据收取费用=月使用费+超时单价×超过时间，可找出关于的函数关系式； （2）将x=60分别代入的表达式中得出值进行比较，即可得出结论． 试题解析：(1)当x≥50时，yA与x之间的函数关系式为yA＝7＋(x－25)×0.6＝0.6x－8， yB与x之间的函数...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学北师大版上册 第1-4章综合测试卷 题型：填空题

    在平面直角坐标系中，O为原点，若一次函数y＝kx＋b的图象交x轴于点A(－2，0)，交y轴于点B，△AOB的面积为8，则该函数解析式为______________．

    y＝4x＋8或y＝－4x－8 【解析】试题解析：设B点的坐标为(0，t)． ∵△AOB的面积为8， ∴×2×|t|＝8，解得t＝8或－8， ∴B点的坐标为(0，8)或(0，－8)． 当直线y＝kx＋b经过A(－2，0)，B(0，8)时，一次函数解析式为y＝4x＋8； 当直线y＝kx＋b经过A(－2，0)，B(0，－8)时，一次函数解析式为y＝－4x－8. ...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学北师大版上册 第1-4章综合测试卷 题型：单选题

    计算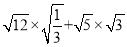的结果在(　　)

    A. 4至5之间 B. 5至6之间 C. 6至7之间 D. 7至8之间

    B 【解析】试题解析：原式 故选B.

    查看答案和解析>>

    科目：初中数学 来源：北师大版九年级下册数学全册综合测试卷一 题型：解答题

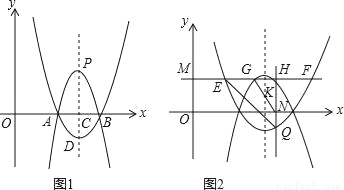
    如图1，二次函数y1=（x﹣2）（x﹣4）的图象与x轴交于A、B两点（点A在点B的左侧），其对称轴l与x轴交于点C，它的顶点为点D．

    （1）写出点D的坐标　 　．

    （2）点P在对称轴l上，位于点C上方，且CP=2CD，以P为顶点的二次函数y2=ax2+bx+c（a≠0）的图象过点A．

    ①试说明二次函数y2=ax2+bx+c（a≠0）的图象过点B；

    ②点R在二次函数y1=（x﹣2）（x﹣4）的图象上，到x轴的距离为d，当点R的坐标为　 　时，二次函数y2=ax2+bx+c（a≠0）的图象上有且只有三个点到x轴的距离等于2d；

    ③如图2，已知0＜m＜2，过点M（0，m）作x轴的平行线，分别交二次函数y1=（x﹣2）（x﹣4）、y2=ax2+bx+c（a≠0）的图象于点E、F、G、H（点E、G在对称轴l左侧），过点H作x轴的垂线，垂足为点N，交二次函数y1=（x﹣2）（x﹣4）的图象于点Q，若△GHN∽△EHQ，求实数m的值．

    （1）（3，﹣1）； （2）①证明见解析；②（3﹣，1）、（3+，1）或（3，﹣1）；③当△GHN∽△EHQ，实数m的值为1． 【解析】（1）∵y1=（x﹣2）（x﹣4）=x2﹣6x+8=（x﹣3）2﹣1， ∴顶点D的坐标为（3，﹣1）．故答案为：（3，﹣1）． （2）①∵点P在对称轴l上，位于点C上方，且CP=2CD，∴点P的坐标为（3，2）， ∴二次函数y1=（x...

    查看答案和解析>>

    同步练习册答案