
已知抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点,若点A的坐标为(-2,0),抛物线的对称轴为直线x=2,则线段AB的长为 .
8 【解析】试题分析:∵对称轴为直线x=2的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点, ∴A、B两点关于直线x=2对称, ∵点A的坐标为(﹣2,0), ∴点B的坐标为(6,0), AB=6﹣(﹣2)=8. 故答案为:8.科目:初中数学 来源:贵州省2017-2018学年八年级(上)期中数学试卷 题型:填空题
如图2,在等腰直角△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于D,DE⊥AB于D,若AB=10,则△BDE的周长等于 .

查看答案和解析>>
科目:初中数学 来源:宁夏吴忠市2018届九年级(上)期中数学试卷 题型:解答题
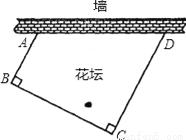
小区要用篱笆围成一个四边形花坛、花坛的一边利用足够长的墙,另三边所用的篱笆之和恰好为18米.围成的花坛是如图所示的四边形ABCD,其中∠ABC=∠BCD=90°,且BC=2AB.设AB边的长为x米.四边形ABCD面积为S平方米.
(1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围).
(2)当x是多少时,四边形ABCD面积S最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源:宁夏吴忠市2018届九年级(上)期中数学试卷 题型:解答题
已知等腰三角形底边长为8,腰长是方程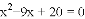 的一个根,求这个等腰三角形的腰长。
的一个根,求这个等腰三角形的腰长。
查看答案和解析>>
科目:初中数学 来源:宁夏吴忠市2018届九年级(上)期中数学试卷 题型:单选题
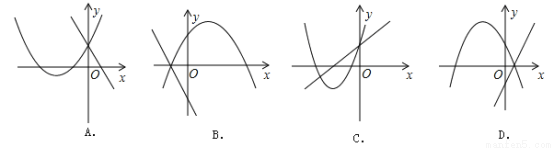
在同一坐标系内,一次函数y=ax+b与二次函数y=ax2+8x+b的图象可能是( )
查看答案和解析>>
科目:初中数学 来源:宁夏吴忠市2018届九年级(上)期中数学试卷 题型:单选题
下列图形绕某点旋转180°后,不能与原来图形重合的是( )

查看答案和解析>>
科目:初中数学 来源:山东省东营市河口区2017-2018学年度第一学期期末考试七年级数学试卷 题型:解答题
已知2a-1的平方根是
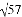 的整数部分,求a+2b+c的算数平方根。
的整数部分,求a+2b+c的算数平方根。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com