
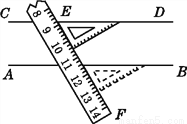
如图,用直尺和三角尺作直线AB,CD,从图中可知,直线AB与直线CD的位置关系为__________,理由是_________.
科目:初中数学 来源:北师大版七年级下册 2.2 探索直线平行的条件(1) 同步练习 题型:填空题
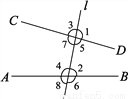
如图,直线AB,CD被直线l所截得到的8个角中,∠1与∠2为同位角,图中的同位角还有∠3与_____,∠5与_____,∠7与_____;
查看答案和解析>>
科目:初中数学 来源:人教版2017-2018学年九年级下册数学全册综合测试卷 题型:填空题
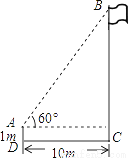
如图,在一次数学课外实践活动中,小聪在距离旗杆10m的A处测得旗杆顶端B的仰角为60°,测角仪高AD为1m,则旗杆高BC为________ m(结果保留根号).
查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下2.2.1 用“同位角、第三直线”判定平行线 同步练习 题型:解答题
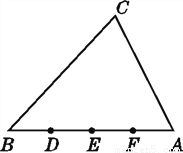
如图,D,E,F是线段AB的四等分点.
(1)过点D作DH∥BC交AC于点H,过点E作EG∥BC交AC于点G,过点F作FM∥BC交AC于点M.
(2)量出线段CH,HG,GM,MA的长度后,你有什么发现?
(3)量出线段HD,EG,FM,BC的长度后,你又有什么发现?
查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下2.2.1 用“同位角、第三直线”判定平行线 同步练习 题型:单选题
在同一平面内,直线m,n相交于点O,且l∥n,则直线l和m的关系是( )
A.平行
B.相交
C.重合
D.以上都有可能
B 【解析】由平行公理可得,直线l和m不可能平行,否则过O有两条直线与直线l平行,而l和m不可能重合,所以l和m必定相交,故选B.查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 全册综合测试卷1 题型:解答题
如图,一次函数y1=kx+b和反比例函数y2=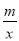 的图象交于A、B两点.
的图象交于A、B两点.
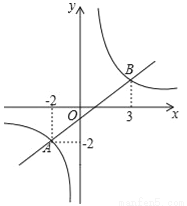
(1)求一次函数y1=kx+b和反比例函数y2=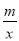 的解析式;
的解析式;
(2)观察图象写出y1<y2时,x的取值范围为 ;
(3)求△OAB的面积.
(1)一次函数的解析式是:y1=x﹣;反比例函数的解析式是:y2=; (2)x<﹣2或0<x<3;(3). 【解析】 试题分析:(1)根据图形得出A、B的坐标,把A的坐标代入反比例函数的解析式,即可求出其解析式;把A、B的坐标代入一次函数的解析式,即可求出一次函数的解析式; (2)根据图象和A、B的横坐标,即可得出答案. (3)求得直线与y轴的交点,然后根据三角形面积...查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 全册综合测试卷1 题型:填空题
如图,在平面直角坐标系中,菱形OABC的面积为12,点B在y轴上,点C在反比例函数y=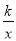 的图象上,则k的值为________.
的图象上,则k的值为________.
查看答案和解析>>
科目:初中数学 来源:江苏省张家港市2017-2018学年第一学期初三数学期末考试试卷 题型:解答题
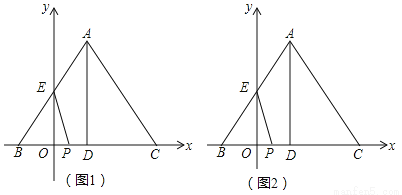
如图,在平面直角坐标系中, 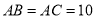 ,线段
,线段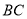 在轴上,
在轴上, 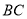 =12,点
=12,点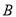 的坐标为(-3,0),线段
的坐标为(-3,0),线段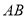 交
交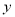 轴于点
轴于点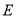 ,过
,过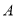 作
作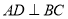 于
于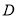 ,动点
,动点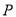 从原点出发,以每秒3个单位的速度沿
从原点出发,以每秒3个单位的速度沿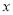 轴向右运动,设运动的时间为
轴向右运动,设运动的时间为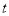 秒.
秒.
(1)点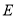 的坐标为(_________),__________);
的坐标为(_________),__________);
(2)当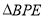 是等腰三角形时,求
是等腰三角形时,求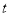 的值;
的值;
(3)若点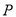 运动的同时,
运动的同时, 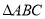 以
以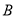 为位似中心向右放大,且点
为位似中心向右放大,且点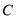 向右运动的速度为每秒2个单位,
向右运动的速度为每秒2个单位, 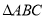 放大的同时高
放大的同时高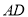 也随之放大,当以
也随之放大,当以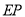 为直径的圆与动线段
为直径的圆与动线段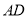 所在直线相切,求
所在直线相切,求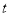 的值和此时C点的坐标.
的值和此时C点的坐标.
查看答案和解析>>
科目:初中数学 来源:2018人教版九年级数学下册练习:期中检测卷 题型:填空题
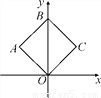
如图,在平面直角坐标系中,正方形OABC的顶点O为坐标原点,点B(0,6),反比例函数y=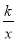 的图象过点C,则k的值为____.
的图象过点C,则k的值为____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com