
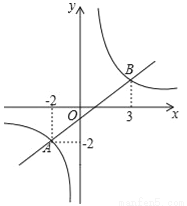
��ͼ��һ�κ���y1=kx+b�ͷ���������y2=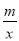 ��ͼ����A��B���㣮
��ͼ����A��B���㣮
��1����һ�κ���y1=kx+b�ͷ���������y2=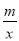 �Ľ���ʽ��
�Ľ���ʽ��
��2���۲�ͼ��д��y1��y2ʱ��x��ȡֵ��ΧΪ ��
��3�����OAB�������
��1��һ�κ����Ľ���ʽ�ǣ�y1=x���������������Ľ���ʽ�ǣ�y2=�� ��2��x����2��0��x��3����3���� �������� �����������1������ͼ�εó�A��B�����꣬��A��������뷴���������Ľ���ʽ��������������ʽ����A��B���������һ�κ����Ľ���ʽ���������һ�κ����Ľ���ʽ�� ��2������ͼ���A��B�ĺ����꣬���ɵó��𰸣� ��3�����ֱ����y��Ľ��㣬Ȼ��������������...
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ����ʦ������꼶�²� 2.2 ̽��ֱ��ƽ�е�������1�� ͬ����ϰ ���ͣ���ѡ��
��ͼ����1��100�㣬Ҫʹa//b����߱�����һ�������� ( )
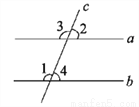
A. ��2��100�� B. ��3��100�� C. ��3��80�� D. ��4��80��
B ���������ߡ�2=100�㣬 �����ƽ���ߵ��ж���֪,����4=100��,���3=100��,���1=80��ʱ,AB��CD. ��ѡ��D.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰�2017-2018ѧ����꼶�²���ѧȫ���ۺϲ��Ծ� ���ͣ���ѡ��
��֪���κ���y=ax2+bx+c��a��0��������M����1��2���͵�N��1����2������x����A��B���㣬��y����C����
��b=��2��
�ڸö��κ���ͼ����y�ύ�ڸ����
�۴�������һ��a��ʹ��M��A��C������ͬһ��ֱ���ϣ�
����a=1����OA•OB=OC2 ��
����˵����ȷ���У�������
A. �٢ڢۢ� B. �ڢۢ� C. �٢ڢ� D. �٢ڢ�
C ���������١߶��κ���y=ax2+bx+c(a>0)������M(?1,2)�͵�N(1,?2)�� �࣬ ���b=?2.�ʸ�ѡ����ȷ�� ���ɢٿɵ�b=?2��a+c=0����c=?a<0�� ���Զ��κ���ͼ����y�ύ�ڸ�����. �ʸ�ѡ����ȷ�� �۸���������ͼ����ص㣬M��A.C���㲻������ͬһ��ֱ����.�ʸ�ѡ����� �ܵ�a=1ʱ��c=?1����������ߵĽ���...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶��ѧ��2.2.1 �á�ͬλ�ǡ�����ֱ�ߡ��ж�ƽ���� ͬ����ϰ ���ͣ���ѡ��
����˵����,�������(����)
����a��c�ཻ,b��c�ཻ,��a��b�ཻ;
����a��b,b��c,��ôa��c;
�۹�ֱ����һ������ֻ��һ��ֱ������ֱ֪��ƽ��;
����ͬһƽ����,����ֱ�ߵ�λ�ù�ϵ��ƽ�С��ཻ����ֱ����.
A. 3�� B. 2�� C. 1�� D. 0��
B ������������a��b�ཻ��b��c�ཻ����a��c�ཻ��ƽ�У��ʱ�С����� ����a��b��b��c����a��c������ƽ�й��������ۣ��������ֱ�߶��͵�����ֱ��ƽ�У���ô����ֱ��Ҳ����ƽ�У�����˵����ȷ�� �۹�ֱ����һ������ֻ��һ��ֱ������ֱ֪��ƽ�У�����ȷ�� ����ƽ���ڣ�����ֱ�ߵ�λ�ù�ϵ��ƽ�к��ཻ���֣��ʲ���ȷ. ���ֻ�Тڢ���ȷ. ��ѡ��B.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶��ѧ��2.2.1 �á�ͬλ�ǡ�����ֱ�ߡ��ж�ƽ���� ͬ����ϰ ���ͣ������
��ͼ,��ֱ�ߺ����dz���ֱ��AB,CD,��ͼ�п�֪,ֱ��AB��ֱ��CD��λ�ù�ϵΪ__________,������_________.
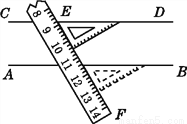
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ��ʦ����ϲ� ȫ���ۺϲ��Ծ�1 ���ͣ������
�����з��̣�
(1)x2��6x��6=0��(2)(x��2)(x��3)=1.
��1��x1=3����x2=3������2��x1=��x2=. ����������������� ��1���á��䷽������˷��̼��ɣ� ��2���á���ʽ������˷��̼���. ��������� (1)x2��6x��6��0�� �䷽�ã�x2��6x��9�� 15�� �� (x��3)2�� 15�� x��3�� �� �� ��x1��3����x2��3��. (2)ԭ���̿ɻ�Ϊ�� �� ���=�� ��...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ��ʦ����ϲ� ȫ���ۺϲ��Ծ�1 ���ͣ������
һ������������ͼ�����A(��2����3)������������������Ľ���ʽ��_________.
y= �����������ݷ���������ͼ���ϵ�������ɵ�: ,���Է����������Ľ���ʽΪ: ,�ʴ�Ϊ: .�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�żҸ���2017-2018ѧ���һѧ�ڳ�����ѧ��ĩ�����Ծ� ���ͣ������
��ͼ����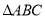 �У���
����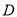 ��
��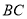 ���ϣ�
���ϣ� 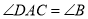 .��
.��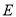 ��
��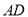 ���ϣ�
���ϣ� 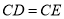 .
.
(1)��֤: 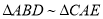 ;
;
(2)��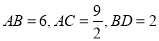 ����
����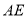 �ij�.
�ij�.
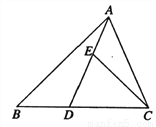
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018�˽̰���꼶��ѧ�²���ϰ�����м��� ���ͣ���ѡ��
��ͼ����ABE�͡�CDE���Ե�E(1��0)Ϊλ�����ĵ�λ��ͼ�Σ���֪��A(3��4)��C(2��2)��D(3��1)�����D�Ķ�Ӧ��B��������( )
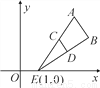
A. (4��2) B. (4��1) C. (5��2) D. (5��1)
C ������������������ֱ��C,D,A,B,��x��Ĵ��ߣ�����ֱ���F,H,K����ΪA,D�ĺ�������ͬ������D��AH�ϣ���E��1,0����C��2��2����A��3��4����D��3��1������EF=1��FH=1����CF��AH��BK,��,��CD��AB,��,��DH��BK,��,��EH=2��DH=1����EK=4��BK=2����OK=5����B��5��2��,��ѡC���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com