练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，⊙O与正方形ABCD的边AB,AD相切，且DE与⊙O 相切与点E,若⊙O 的半径为5，

    且AB=12，则DE=（ ）

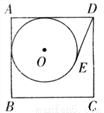
    A. 5 B. 6 C. 7 D.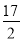

    C 【解析】【解析】 连接OM、ON．∵四边形ABCD是正方形，∴AD=AB=12，∠A=90°．∵圆O与正方形ABCD的两边AB、AD相切，∴∠OMA=∠ONA=90°=∠A．∵OM=ON，∴四边形ANOM是正方形，∴AM=OM=5．∵AD和DE与圆O相切，圆O的半径为5，∴AM=5，DM=DE，∴DE=12﹣5=7．故选C．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：安徽省宿州市（城西校区） 2017-2018学年九年级第一学期期中测试数学试卷 题型：单选题

    为解决群众看病贵的问题，有关部门决定降低药价，对某种原价为289元的药品进行连续两次降价后为256元，设平均每次降价的百分率为x，则下面所列方程正确的是( )

    A. 289(1-x)2=256

    B. 256(1-x)2=289

    C. 289（1-2x)=256

    D. 256(1-2x)=289

    A 【解析】 试题分析：第一次降价后的价格为289(1-x)，第一次降价后的价格为289(1-x)（1-x),即289(1-x)2=256； 故选A.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年北师大版八年级数学下册 期末测评 题型：单选题

    如图，∠AOP=∠BOP=15°，PC∥OA，PD⊥OA，若PC=4，则PD的长为_____．

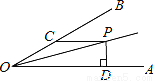
    2 【解析】试题分析：过P作PE⊥OB于E，根据角平分线的性质可得PE=PD，在求得∠BCP=30°，在Rt△ECP中，根据30°的锐角所对的直角边等于斜边的一半即可求得PD的长． 试题解析： 过P作PE⊥OB于E， ∵PD⊥OA，PE⊥OB，∠AOP=∠BOP=15°，∴∠BOA=30°，PE=PD， ∵PC∥OA，∴∠BOA=∠BCP=30°， 又△ECP为...

    查看答案和解析>>

    科目：初中数学 来源：辽宁省2018届九年级上学期期末考试数学试卷 题型：解答题

    某校9年2班有2名男生和3名女生报名参加志愿者活动。若从报名者中随机选取2名学生参加志愿者活动，请你用列表法或画树状图求选取的两名学生是一男一女的概率

    【解析】试题分析：列举出所有情况，看选取的两名学生是一男一女的情况数占总情况数的多少即可． 试题解析：【解析】 画树状图如图： 由树状图可得出：共有20种情况，由树状图可知共有20种等可能结果，其中选取的2名学生是一男一女的结果有12种，所以概率为 ．

    查看答案和解析>>

    科目：初中数学 来源：辽宁省2018届九年级上学期期末考试数学试卷 题型：填空题

    在4张完全相同的卡片上分别画上①、②、③、④ 。在看不见图形的情况下随机抽取一

    张，卡片上的图形为中心对称图形的概率是__________

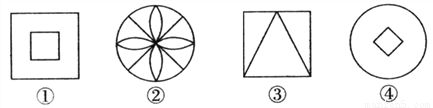
    【解析】先判断图中中心对称图形的个数，再根据概率公式进行解答即可． 【解析】 ∵在这一组图形中中心对称图形的是：①②④共3个， ∴卡片上的图形是中心对称图形的概率是3/4． 故答案为：3/4． 本题主要考查的是概率公式及中心对称图形，如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=m/n．

    查看答案和解析>>

    科目：初中数学 来源：辽宁省2018届九年级上学期期末考试数学试卷 题型：单选题

    一元二次方程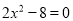的解 是（ ）

    A. x=2 B. x=-2 C. 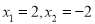D.

    C 【解析】【解析】 ， ， ，∴x=±2．故选C．

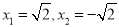
    查看答案和解析>>

    科目：初中数学 来源：浙江省宁波市东海实验学校2017年中考数学模拟试卷 题型：解答题

    已知x=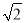+1，求x+1﹣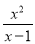的值．

    原式=，当x= +1时，原式=﹣． 【解析】试题分析：本题考查了分式的化简求值，先通分，化成同分母的分式相加减，然后约分化成最简分式，最后代入求值. =， 当时， 原式=﹣．

    查看答案和解析>>

    科目：初中数学 来源：浙江省宁波市东海实验学校2017年中考数学模拟试卷 题型：单选题

    关于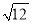的下列说法中错误的是（ ）

    A. 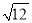是无理数 B. 3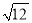＜＜4

    C. 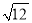是12的算术平方根 D. 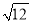不能化简

    D 【解析】A. 是一个无理数，故A正确，与要求不符； B. 9<<16,故3<<4，故B正确，与要求不符； C. 是12的算术平方根，故C正确，与要求不符； D. =，故D错误，与要求相符。 故选：D.

    查看答案和解析>>

    科目：初中数学 来源：2017年辽宁省中考数学二模试卷 题型：填空题

    若关于x的函数y=（a+2）x2﹣（2a﹣1）x+a﹣2的图象与坐标轴有两个交点，则a的值为_____．

    ﹣2，2或 【解析】∵关于x的函数y=（a+2）x2﹣（2a﹣1）x+a﹣2的图象与坐标轴有两个交点， ∴可分如下三种情况： ①当函数为一次函数时，有a+2=0， ∴a=﹣2，此时y=5x﹣4，与坐标轴有两个交点； ②当函数为二次函数时（a≠﹣2），与x轴有一个交点，与y轴有一个交点， ∵函数与x轴有一个交点， ∴△=0， ∴（2a﹣1）2﹣4（a+...

    查看答案和解析>>

    同步练习册答案