
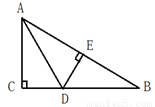
如图:△ABC中,∠C=90°,AD 平分∠BAC交CB于点D.现将直角边AC沿直线AD折叠,AC边恰好落在斜边上,且点C与斜边AB的中点E刚好重合,若CD=3,则BD=________________.
科目:初中数学 来源:初一数学第一学期4.1线段、直线、射线 同步练习 题型:填空题
已知n(n≥2)个点P1,P2,P3,…,Pn在同一平面内,且其中没有任何三点在同一直线上.设Sn表示过这n个点中的任意2个点所作的所有直线的条数,显然,S2=1,S3=3,S4=6,S5=10,…,由此推断,Sn=__.
【解析】本题考查了找规律的能力 分析数据后总结规律,再进行计算. ,,,查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期人教版八年级数学上11.2.1《三角形的内角和》同步练习题(含答案) 题型:单选题
一个三角形三个内角的度数之比为2∶3∶7,这个三角形一定是( )
A. 等腰三角形 B. 直角三角形 C. 锐角三角形 D. 钝角三角形
D 【解析】试题解析:∵一个三角形三个内角的度数之比为2:3:7, ∴这个三角形的最大角为:180°×=105°, ∴这个三角形一定是钝角三角形. 故选C.查看答案和解析>>
科目:初中数学 来源:2018年春九年级数学下册湘教版:单元测试(四) 概率 题型:单选题
用1、2、3三个数字组成一个三位数,则组成的数是偶数的概率是( )
A. 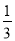 B.
B. 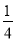 C.
C. 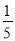 D.
D. 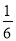
查看答案和解析>>
科目:初中数学 来源:山西省大同市矿区2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
在学习了全等三角形和等边三角形的知识后,张老师出了如下一道题:如图,点B是线段AC上任意一点,分别以AB、BC为边在AC同一侧作等边△ABD和等边△BCE,连接CD、AE分别与BE和DB交于点N、M,连接MN.
(1)求证:△ABE≌△DBC.
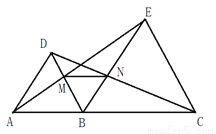
接着张老师又让学生分小组进行探究:你还能得出什么结论?
精英小组探究的结论是:AM=DN.
奋斗小组探究的结论是:△EMB≌△CNB.
创新小组探究的结论是:MN∥AC.
(2)你认为哪一小组探究的结论是正确的?
(3)选择其中你认为正确的一种情形加以证明.
(1)证明见解析;(2)三个小组探究的结论都正确;(3)证明见解析 【解析】试题分析: (1)由△ABD和△BCE都是等边三角形可得:AB=DB,BC=BE,∠ABD=∠EBC=60°,这样可得∠ABE=∠DBC,从而可由“SAS”证得△ABE≌△DBC; (2)由△ABE≌△DBC可得∠EAB=∠CDB,而由已知条件易证∠DBN=∠ABD=60°,结合AB=DB可证△ABM≌△...查看答案和解析>>
科目:初中数学 来源:山西省大同市矿区2017-2018学年八年级上学期期中考试数学试卷 题型:填空题
一副分别含30°和45°角的两个直角三角板拼成如图所示的图形,其中∠C=90°,∠B=45°,∠E=30°.则∠AFE=______________.
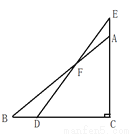
查看答案和解析>>
科目:初中数学 来源:山西省大同市矿区2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
根据下列条件,只能画出唯一的△ABC的是( )
A. AB=3 BC=4 B. AB=4 BC=3 ∠A=30°
C. ∠A=60°∠B=45° AB=4 D. ∠C=60°AB=5
C 【解析】由所给边、角条件只能画出唯一的△ABC,说明当按所给条件画两次时,得到的两个三角形是全等的,即所给条件要符合三角形全等的判定方法;而在四个选项中,当两个三角形分别满足A、B、D三个选项中所列边、角对应相等时,两三角形不一定全等;当两个三角形满足C选项中所列边、角对应相等时,三角形是一定全等的. 故选C.查看答案和解析>>
科目:初中数学 来源:2017年秋(北师大版)九年级数学下册(河南)检测:3.9 弧长及扇形的面积 题型:单选题
120°的圆心角对的弧长是6π,则此弧所在圆的半径是( )
A. 3 B. 4 C. 9 D. 18
C 【解析】试题分析:已知120°的圆心角对的弧长是6π,根据弧长的公式l=可得6π=,解得r=9.故答案选C.查看答案和解析>>
科目:初中数学 来源:湖南省醴陵市青云学校2016-2017学年七年级上学期期中考试数学试卷 题型:单选题
A. 2016 B. ﹣2016 C. ±2016 D. 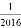
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com