
科目:初中数学 来源:台湾省2018年中考数学试卷 题型:解答题
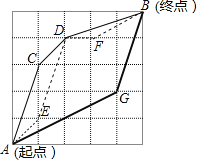
嘉嘉参加机器人设计活动,需操控机器人在5×5的方格棋盘上从A点行走至B点,且每个小方格皆为正方形,主办单位规定了三条行走路径R1,R2,R3,其行经位置如图与表所示:
路径 | 编号 | 图例 | 行径位置 |
第一条路径 | R1 | _ | A→C→D→B |
第二条路径 | R2 | … | A→E→D→F→B |
第三条路径 | R3 | ▂ | A→G→B |
已知A、B、C、D、E、F、G七点皆落在格线的交点上,且两点之间的路径皆为直线,在无法使用任何工具测量的条件下,请判断R1、R2、R3这三条路径中,最长与最短的路径分别为何?请写出你的答案,并完整说明理由.
查看答案和解析>>
科目:初中数学 来源:安徽省2017-2018学年度下期八年级期末考试数学试卷 题型:单选题
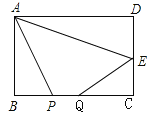
如图,在矩形ABCD中 ,AB=4,BC=8,点E为CD中点,P、Q为BC边上两个动点,且PQ=2,当四边形APQE周长最小时,BP的长为( )
A. 1 B. 2 C. 2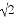 D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源:甘肃省2017-2018学年七年级下学期第二次月考数学试卷 题型:单选题
小燕子要在鱼缸里饲养
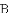
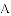
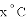 的范围是
的范围是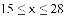
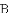
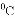 的范围是
的范围是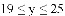
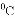 应该设定在( )
应该设定在( )
A. 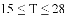
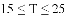
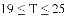
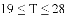
查看答案和解析>>
科目:初中数学 来源:2017-2018学年泰兴市 初二数学下学期期末试卷 题型:解答题
)矩形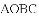
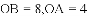
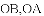
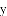
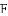
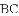
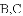
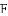
 (
(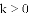
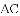
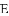
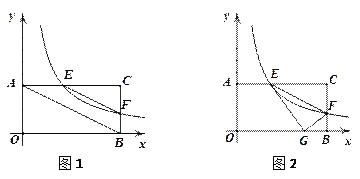
(1)当点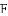
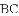
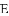
(2)连接EF、AB,求证:EF∥AB;
(3)如图2,将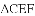
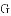
查看答案和解析>>
科目:初中数学 来源:2017-2018学年泰兴市 初二数学下学期期末试卷 题型:解答题
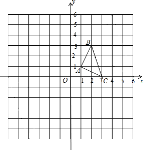
如图,△ABC的顶点坐标分别为A(1,1),B(2,3),C(3,0).(1)画出△ABC绕点O逆时针旋转90°后得到的△DEF;
(2)以点O为位似中心,在第三象限内把△ABC按相似比2:1放大(即所画△PQR与△ABC的相似比为2:1).
(3)在(2)的条件下,若M(a,b)为△ABC边上的任意一点,则△PQR的边上与点M对应的点M′的坐标为 .
查看答案和解析>>
科目:初中数学 来源:四川省内江市2018年中考数学试卷 题型:解答题
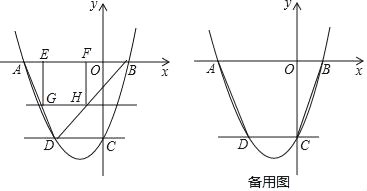
如图,已知抛物线y=ax2+bx﹣3与x轴交于点A(﹣3,0)和点B(1,0),交y轴于点C,过点C作CD∥x轴,交抛物线于点D.
(1)求抛物线的解析式;
(2)若直线y=m(﹣3<m<0)与线段AD、BD分别交于G、H两点,过G点作EG⊥x轴于点E,过点H作HF⊥x轴于点F,求矩形GEFH的最大面积;
(3)若直线y=kx+1将四边形ABCD分成左、右两个部分,面积分别为S1,S2,且S1:S2=4:5,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com