
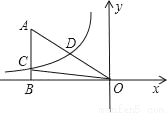
如图,已知双曲线y= (k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣6,4),则△AOC的面积为( )
(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣6,4),则△AOC的面积为( )
A. 12 B. 9 C. 6 D. 4
B 【解析】试题分析:△AOC的面积=△AOB的面积-△BOC的面积,由点A的坐标为(-6,4),根据三角形的面积公式,可知△AOB的面积=12,由反比例函数的比例系数k的几何意义,可知△BOC的面积=|k|.只需根据OA的中点D的坐标,求出k值即可. 试题解析:∵OA的中点是D,点A的坐标为(-6,4), ∴D(-3,2), ∵双曲线y=经过点D, ∴k=-3×2=...科目:初中数学 来源:人教版初中数学七年级下册第六章 《平方根》同步练习 题型:解答题
计算下列各式的值.
(1)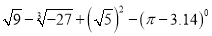 (2) 求x的值:
(2) 求x的值: 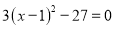
查看答案和解析>>
科目:初中数学 来源:人教版初中数学七年级下册第八章《二元一次方程组》同步练习 题型:解答题
已知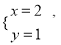 是二元一次方程组
是二元一次方程组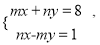 的解,求2m-n的算术平方根.
的解,求2m-n的算术平方根.
查看答案和解析>>
科目:初中数学 来源:山东省临沂市经济开发区2018届九年级上学期期末考试数学试卷 题型:解答题
如图,直线y=﹣x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.
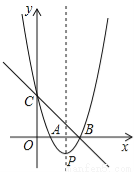
(1)求该抛物线的解析式;
(2)连接AC,在x轴上是否存在点Q,使以P、B、Q为顶点的三角形与△ABC相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
(1)抛物线解析式为y=x2﹣4x+3;(2)Q点的坐标为(0,0)或(,0). 【解析】试题分析:(1)先确定出点B,C坐标,再用待定系数法求函数解析式; (2)先求出BA=2,BC=3,BP=,然后分两种情况①由△ABC∽△PBQ,得到,求出BQ,②由△ABC∽△QBP得,求出BQ,即可. 【解析】 (1)∵直线y=﹣x+3与x轴、y轴分别交于点B、点C, 令x=0,...查看答案和解析>>
科目:初中数学 来源:山东省临沂市经济开发区2018届九年级上学期期末考试数学试卷 题型:填空题
如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为 .
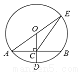
查看答案和解析>>
科目:初中数学 来源:山东省临沂市经济开发区2018届九年级上学期期末考试数学试卷 题型:单选题
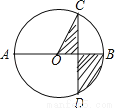
如图,AB是⊙O的直径,CD⊥AB,∠ABD=60°,CD=2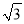 ,则阴影部分的面积为( )
,则阴影部分的面积为( )
A. 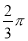 B. π C. 2π D. 4π
B. π C. 2π D. 4π
查看答案和解析>>
科目:初中数学 来源:2018届中考数学一轮复习单元检测:第6讲 分式方程及其应用 题型:解答题
甲、乙两个工程队均参与某筑路工程,先由甲队筑路60千米,再由乙队完成剩下的筑路工程,已知乙队筑路总千米数是甲队筑路总千米数的 倍,甲队比乙队多筑路20天.
倍,甲队比乙队多筑路20天.
(1)求乙队筑路的总千米数;
(2)若甲、乙两队平均每天筑路千米数之比为5∶8,求乙队平均每天筑路多少千米
(1) 80千米;(2) 千米 【解析】试题分析:(1)根据乙队筑路总千米数是甲队筑路总千米数的倍列式计算即可得; (2)设甲队平均每天筑路5x千米,则乙队平均每天筑路8x千米,根据题意可得等量关系:甲队筑路用的天数-20=乙队筑路用的天数,列出方程解方程即可. 试题解析:(1)60× =80(千米),即乙队筑路的总千米数为80千米. (2)设甲队平均每天筑路5x千米,则乙...查看答案和解析>>
科目:初中数学 来源:广西北海市银海区2017年秋季学期教学质量监测七年级数学试卷 题型:解答题
A、B两地相距216千米,甲、乙分别在A、B两地,若甲骑车的速度为15千米/时,乙骑车的速度为12千米/时。.
(1)甲、乙同时出发,背向而行,问几小时后他们相距351千米?
(2)甲、乙相向而行,甲出发三小时后乙才出发,问乙出发几小时后两人相遇?
(3)甲、乙相向而行,要使他们相遇于AB的中点,乙要比甲先出发几小时?
(4)甲、乙同时出发,相向而行,甲到达B处,乙到达A处都分别立即返回,几小时后相遇?相遇地点距离A有多远?
(1) 5;(2);(3) 1.8小时;(4) 24小时后相遇地点距离A有72千米. 【解析】试题分析:根据相遇问题的等量关系为:两者的路程之和=相距总路程,设未知数,列方程求解即可. 试题解析:【解析】 (1)设经过x小时后他们相距351千米,根据题意得: 15x+12x=351-216 解得:x=5 答:经过5小时后他们相距351千米. (2)设相向而行,...查看答案和解析>>
科目:初中数学 来源:人教版九年级下册数学 第26章 反比例函数 单元检测卷 题型:单选题
三角形的面积为12cm2 , 这时底边上的高ycm底边xcm之间的函数关系用图象表示大致是( )
A. 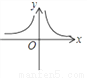 B.
B.  C.
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com